Berikut bentuk umum fungsi kuadrat
f(x) = ax² + bx + c
atau dalam bentuk koordinat kartesius
⇔ y = ax² + bx + c
atau dalam bentuk relasi fungsi
f : x → ax² + bx + c
dengan
a = koefisien variabel x², dengan a ≠ 0
Dan untuk pertemuan hari ini, kita akan membahas materi lanjutan yaitu Menentukan Titik Puncak dan Sumbu Simetri Fungsi Kuadrat dan lebih jelas nya dalam memahami materi hari ini silahkan kalian baca dan pahami pembahasan materi berikut :
Grafik Fungsi Kuadrat
Nah,
kini saatnya kita mengetahui apa itu grafik fungsi kuadrat,
yaitu yaitu suatu grafik yang berguna untuk menguraikan gambaran dari
fungsi kuadrat.
Kemudian, ciri-ciri grafik fungsi kuadrat bisa kamu simak seperti di bawah ini.
- Memiliki grafik yang simetris.
- Bentuknya identik seperti parabola.
- Hanya memiliki titik minimum saja atau titik maksimum saja, tidak keduanya.
- Adanya yang merupakan variabel terikat. Sementara itu, variabel bebasnya adalah , dan a serta b adalah koefisien yang variabel dengan pangkat paling tinggi yakni dua serta berbentuk persamaan.
Kemudian, grafik ini juga memiliki beberapa sifat serta cara menyusunnya, yaitu sebagai berikut:
1. Grafik Terbuka
Sifat
yang satu ini grafiknya ditentukan oleh nilai f yang berfungsi untuk
menentukan hasil ke arah bawah ataupun ke arah atas. Apabila a>0,
maka grafiknya akan menampakkan atas.
Sementara itu, apabila nilai a<0, maka hasil grafiknya negatif atau ke bawah.
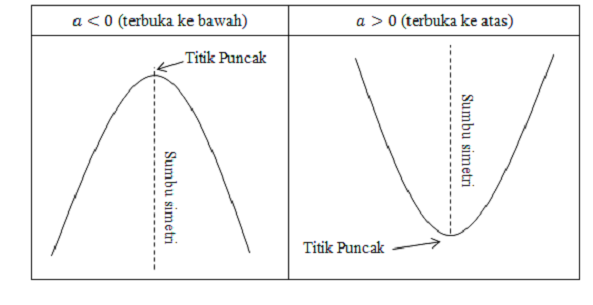
2. Titik Puncak
Sifat
ini dapat kamu lihat ketika grafik memperlihatkan hasil ke bawah. Jadi,
titik puncaknya berada pada titik maksimum. Kemudian, apabila grafik
mengarah ke atas serta terbuka, maka minimum adalah titik puncaknya.
Apabila kalian sudah mengetahui bahwa rumus fungsi kuadrat adalah , maka titik puncak grafik bisa kamu ketahui dengan rumus:
Dengan keterangan:
= posisi titik puncak pada sumbu
= posisi titik puncak pada sumbu
= koefisien
b = koefisien
D = diskriminan
3. Sumbu Simetri
Titik
puncak pada grafik akan terbagi menjadi dua bagian karena adanya sumbu
simetri. Pada fungsi kuadrat, sumbu simetri ini berfungsi sebagai sebuah
garis cermin pada titik grafik. Sumbu simetri dapat kamu hitung
menggunakan rumus perhitungan sumbu x, yaitu:
4. Titik Potong Sumbu Y
Pengertiannya
yakni titik yang akan memotong sumbu X. Grafik yang mempunyai sumbu ini
umumnya akan memunculkan persamaan kuadrat.
5. Titik Potong Sumbu X
Sifat terakhir dari grafik fungsi kuadrat adalah titik potong sumbu X.
Setelah
memahami sifat-sifatnya, kini menggambarkan grafik menjadi lebih mudah.
Adapun acara menyusun persamaan grafik fungsi kuadrat yakni sebagai
berikut:
- Ketahui dulu tiga titik koordinat menggunakan persamaan
- Setelah itu, ketahui juga titik potong yang ada pada sumbu serta titik yang dilewatkan mengaplikasikan rumus
- Ketahui pundak serta satu titiknya menggunakan rumus
Soal Fungsi Kuadrat
Penjelasan
di atas tentunya sudah cukup jelas, untuk lebih memahami fungsi
kuadrat, simak contoh soal beserta penyelesaiannya berikut ini:
1. Contoh Soal 1
Diketahui jika grafik . Maka, tentukanlah titik potong grafik pada sumbu x!
Jawab:
Grafik akan memotong sumbu apabila , maka:
dan
dan
dan
Dengan demikian, titik potong grafik tersebut pada sumbu yakni dan (-2, 0)
2. Contoh Soal 2
Diketahui grafik . Tentukanlah titik poting grafik pada sumbu !
Jawab:
Grafik dan memotong sumbu apabila , maka:
Maka, adalah -6.
Dengan demikian, titik potong grafik tersebut pada sumbu adalah (0, -6).
3. Contoh Soal 3
Pabrik tekstil ingin memproduksi potong celana. Biaya produksi yang diperlukan dijabarkan dalam fungsi dalam ratusan ribu rupiah. Lalu, hitunglah biaya minimum yang dibutuhkan dalam memproduksi celana tersebut.
Jawab:
dapat diketahui jika nilai a dalah 3, nilai b adalah -30, dan nilai c adalah 175.
Maka, koordinat titik minimumnya bisa ditentukan menggunakan .
Untuk menjadi nilai x-nya, dapat menggunakan persamaan , sehingga didapatkan:
Jadi, , sehingga didapat x dalah 5.
4. Contoh Soal 4
Pada suatu fungsi kuadrat dengan titik puncak (2, 3). Maka, tentukan nilai dari !
Jawab:
Substitusikan koordinat x di titik puncak pada rumus sumbu simetri. Hal ini berguna untuk mengetahui berapa nilai a, yaitu:
Dengan demikian, a adalah 2.
Kemudian, substitusikan nilai a dengan koordinat puncak, yakni (2,3) pada fungsi kuadrat
Untuk mengetahui nilai c, dengan uraian sebagai berikut:
Maka, . Dengan demikian nilai c adalah 10.
Kemudian, untuk menemukan nilai dengan mensubtitusikan dan nilai serta ke dalam , yaitu:
Dengan demikian nilai f(3) adalah 4.
Demikian penjelasan mengenai Titik Puncak dan Sumbu Simetri Fungsi Kuadrat . Kesimpulan yang dapat kita ambil dari pembelajaran kita hari ini adalah
rumus fungsi kuadrat adalah , maka titik puncak grafik bisa kamu ketahui dengan rumus:
Semoga
dengan penjelasan dan contoh di atas , kalian akan bertambah ilmunya
dan dapat memahami nya. Jika ada yang ingin ditanyakan silahkan isi
kolom kometar di bawah ini..
Wassalamualaikum Warrohmatullahi Wabarrohkatuh..
Sumber : https://www.pijarbelajar.id/blog/fungsi-kuadrat






