KEKONGRUENAN DUA SEGITIGA

 Senin - Kamis, 17 - 19 Januari 2022

Guru            : Fara Dibah, S.Pd

Mapel          : Matematika

Kelas           : IX E, F, G

 

Kode KD     : 

3.6 Menjelaskan Kesebangunan dan Kekongruenan

4.6 Menyelesaikan masalah konstektual yang berkaitan dengan Kesebangunan dan Kekongruenan

Materi          : Kekongruenan Dua Segitiga

Tujuan          : 

1. Peserta didik dapat menyimpulkan tentang Kesebangunan Dua Segitiga

2. Peserta didik dapat menyelesaikan masalah konstektual yang berkaitan dengan Kesebangunan Dua Segitiga

Assalamualaikum Warromatullahi Wabarrohkatuh..

Selamat pagi Semua !

Bagaimana Kabar Soleh/Soleha hari ini  ?…

Semoga kita semua dalam lindungan Allah SWT. Aamiin ..

Selamat datang di pembelajaran semester genap, kalian harus tetap semangat ya nak ..

Baiklah Soleh/Soleha, Pertemuan hari ini kita membahas tentang Kekongruenan Dua Segitiga. Silahkan di simak materi ibu berikut ini : 

Kongruen Dua Segitiga

Kongruen dilambangkan dengan 

≅, sehingga jika terdapat dua buah segitiga yang kongruen misalnya ΔABC kongruen dengan ΔPQR, maka dapat ditulis sebagai ΔABC≅ΔPQR.

Perhatikan gambar berikut.

Dari gambar di atas diketahui bahwa ΔACM adalah segitiga sama kaki. Sisi AP merupakan garis tinggi ΔACM, sehingga membentuk ΔACP dan ΔAMP. Apakah ΔACP kongruen dengan ΔAMP? ΔACP kongruen dengan ΔAMP (ΔACP ≅ ΔAMP) karena:

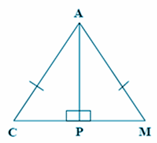
• ΔACP dapat tepat menempati ΔAMP dengan cara mencerminkan ΔACP terhadap garis AP atau semua sisi ΔACP memiliki panjang yang sama dengan ΔAMP.
• ΔCAM merupakan segitiga sama kaki, sehingga ∠ACP = ∠AMP (sudut pada kaki segitiga samakaki ΔCAM) dan ∠APC = ∠APM = 90⁰. Ini berakibat ∠CAP = ∠MAP.

Dari uraian di atas diperoleh kesimpulan sebagai berikut.

Sifat-Sifat Dua Segitiga yang Kongruen

• Sisi–sisi yang bersesuaian mempunyai panjang yang sama
• Sudut–sudut yang seletak besarnya sama

Syarat-Syarat Dua Segitiga yang Kongruen

• Dua segitiga akan kongruen jika ketiga sisi yang bersesuaian dari dua segitiga itu sama panjang (s, s, s).

       Perhatikan jajargenjang PQRS. Garis QS merupakan diagonal jajargenjang PQRS yang membaginya menjadi 2 buah segitiga yaitu ΔPQS dan ΔRSQ. Apakah ΔPQS kongruen dengan ΔRSQ? Pada jajargenjang PQRS, sisi-sisi yang berhadapan sejajar dan sama panjang yaitu:

PQ // SR sehingga PQ = SR
PS // QR sehingga PS = QR.

Selanjutnya, QS adalah diagonal bidang sehingga QS = SQ. Dengan demikian, sisi-sisi yang bersesuaian dari ΔPQS dan ΔRSQ sama panjang. Jadi, ΔPQS dan ΔRSQ kongruen.

• Dua segitiga akan kongruen jika dua sisi pada segitiga pertama sama panjang dengan dua sisi yang bersesuaian pada segitiga kedua, dan besar sudut apit dari kedua sisi tersebut sama (s, sd, s).

       Pada gambar tersebut, sisi DE = KL, ∠D = ∠K, dan DF = KM. Jika kita mengukur panjang sisi dan besar sudut lainnya yaitu sisi EF dan LM, ∠E dan ∠L, serta ∠F dan ∠M, maka akan diperoleh:

EF = LM
∠E = ∠L
∠F = ∠M.

Dengan demikian, pada ΔDEF dan ΔKLM berlaku panjang DE = KL, EF = LM, dan DF = KM. ini berati bahwa pada ΔDEF dan ΔKLM sisi-sisi yang bersesuaian sama panjang. Selain itu, besar ∠D = ∠K, ∠E = ∠L, dan ∠F = ∠M. Ini berarti bahwa sudut-sudut yang bersesuaian sama besar. Hal ini menunjukkan bahwa ΔDEF dan ΔKLM memenuhi sifat dua segitiga yang kongruen.

• Dua segitiga akan kongruen jika dua sudut pada segitiga pertama sama besar dengan dua sudut yang bersesuaian pada segitiga kedua, dan sisi yang merupakan kaki persekutuan kedua sudut sama panjang (sd, s, sd).

       Pada gambar tersebut, ∠G = ∠X, ∠H = ∠Y, dan sisi GH = XY. Jika kita mengukur besar ∠I dan ∠Z, panjang sisi GI dan XZ, serta panjang HI dan YZ, maka akan diperoleh:

besar ∠I = ∠Z
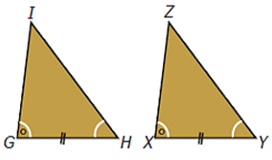
panjang sisi GI = XZ
panjang HI = YZ.

Dengan demikian, pada ΔGHI dan ΔXYZ berlaku, ∠G = ∠X, ∠H = ∠Y, dan ∠I = ∠Z. Ini berati bahwa pada ΔGHI dan ΔXYZ sudut-sudut yang bersesuaian sama besar. Panjang GH = XY, HI = YZ, dan GI = XZ. Ini berarti bahwa pada ΔGHI dan ΔXYZ sisi-sisi yang bersesuaian sama panjang. Hal ini menunjukkan bahwa ΔGHI dan ΔXYZ memenuhi sifat dua segitiga yang kongruen.

Perbedaan antara Kesebangunan dan Kekongruenan pada Segitiga

Contoh 1

Perhatikan gambar berikut.

Jika ΔABC kongruen dengan ΔPQR, maka tentukan:
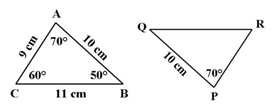
- panjang PR
- panjang QR
- ∠PQR
- ∠QRP

Penyelesaian:

• Oleh karena sisi PR bersesuaian dengan AC, maka panjang sisi PR = AC = 9 cm.
• Oleh karena sisi QR bersesuaian dengan CB, maka panjang QR = CB = 11 cm.
• Oleh karena ∠PQR bersesuaian dengan ∠ABC, maka ∠PQR = ∠ABC = 50⁰.
• Oleh karena ∠QRP bersesuaian dengan ∠ACB, maka ∠ QRP = ∠ ACB = 60⁰.

Contoh 2

Perhatikan gambar segitiga siku-siku di bawah ini.

Tentukan nilai x yang memenuhi agar segitiga siku-siku ABC kongruen dengan segitiga siku-siku PQR.

Penyelesaian:

Dua segitiga dikatakan kongruen jika semua sisi yang besesuaian sama panjang. Oleh karena itu, sisi AB = PQ, AC = PR dan BC = QR.

Panjang sisi BC dapat ditentukan dengan menggunakan teorema Pythagoras, yaitu:

BC2=AB2+AC2$B{C}^2=A{B}^2+A{C}^2$

⇔BC=AB2+AC2−−−−−−−−−−√$\iff BC=\sqrt{A{B}^2+A{C}^2}$

⇔BC=62+82−−−−−−√$\iff BC=\sqrt{6^2+8^2}$

⇔BC=36+64−−−−−−√$\iff BC=\sqrt{36+64}$

⇔BC=100−−−√$\iff BC=\sqrt{100}$

⇔BC=10$\iff BC=10$

⇔BC=QR$\iff BC=QR$

⇔10=3+x$\iff 10=3+x$

⇔x=10−3=7$\iff x=10-3=7$ cm

Jadi, nilai x yang memenuhi agar segitiga siku-siku ABC kongruen dengan segitiga siku-siku PQR adalah 7 cm.

setelah kalian menyimak materi di atas silahkan kalian kerjakan Tugas Rumah Halaman 179 (Buku Hijau) Bagian B No 1 dan 2.

silahkan di kumpul paling lambat hari Kamis 20 Januari 2022, dan akan dinilai serta di bahas saat pertemuan tatap muka.

terimakasih dan tetap semangat ..

Wassalamualaikum Wr. Wb

Referensi : https://www.danlajanto.com/2016/08/kekongruenan-pada-segitiga.html