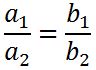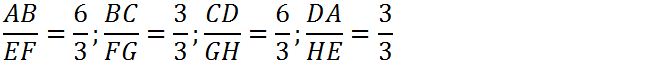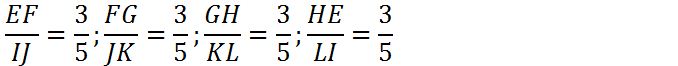IDENTITAS
Mata Pelajaran : Matematika
Kelas : IX C
Pertemuan : Ke4
Materi : Kesebangunan Pada Segitiga
Guru Pengampu : Fara Dibah, S.Pd
Waktu Pembelajaran: Senin, 23 Februari 2026
Alat Peraga : Buku Berpetak, Pensil, Penggaris
Media Pembelajaran : LCD Proyektor dan Laptop
Capaian Pembelajaran :
Diakhir Fase D, peserta didik dapat menjelaskan sifat-sifat kekongruenan dan kesebangunan pada segitiga dan segiempat, serta menggunakannya untuk menyelesaikan masalah.
Kompetensi Inti :
1. Menjelaskan Kesebangunan dan Kekongruenan pada segiempat dan segitiga
2. Menyelesaikan masalah konstektual yang berkaitan dengan Kesebangunan dan Kekongruenan pada segitiga dan segiempat
Tujuan :
1. Peserta didik mampu menjelaskan
dan menentukan kesebangunan dan kekongruenan antar bangun datar
2. Peserta didik mampu menyelesaikan
masalah yang berkaitan dengan kesebangunan dan kekongruenan antar bangun datar
Assalamualaikum Warromatullahi Wabarrohkatuh..
Selamat pagi Semua !
Bagaimana Kabar Soleh/Soleha hari ini ?…
Semoga kita semua dalam lindungan Allah SWT. Aamiin ..
Soleh/soleha apakah tadi subuh kalian sudah melaksanakan solat subuh tepat waktu ? untuk yang laki-laki solat subuh nya di masjid atau di musholla ya nak, agar kita mendapat keberkahan dari Allah SWT ..
Dan untuk yang perempuan silahkan solat subuh nya secara munfarid dirumah masing-masing..
Materi Pembelajaran :
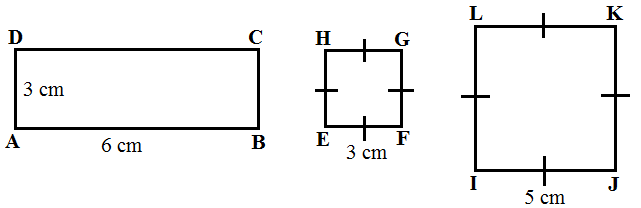
Pada pertemuan sebelumnya, kita sudah mempelajari Konsep Kesebangunan dan Kekongruenan Bangun Datar. Kesebangunan bangun datar di mana sudut – sudutnya mempunyai kesesuaian yang sama besarnya. Dan juga panjang sisi – sisi sudutnya juga bersesuai dengan mempunyai sebuah perbandingan yang sama. sedangkan Kekongruenan merupakan dua buah bangun datar yang di mana kedua bangunnya sama – sama memiliki bentuk dan juga ukuran yang sama.
Dan pada hari ini kita akan membahas tentang Kesebangunan Dua Segitiga, silahkan kalian simak materi berikut ini:
sumber : https://www.youtube.com/watch?v=BzYhJfNOpiw
Secara umum dua buah bangun datar dikatakan sebangun (similar) jika sisi-sisi yang bersesuaian mempunyai perbandingan yang sama. Khusus untu segitiga sebagai bangun datar poligon dengan jumlah sisi paling sedikit, asal dua buah segitiga sudut-sudutnya sama besar maka sudah sebangun.
Kita perhatikan dua buah segitiga sebangun berikut :
sebangun dengan karena :
,
,
.
Lebih lanjut karena :
menghadap sisi BC dan menghadap sisi QR,
menghadap sisi AC dan menghadap sisi PR,
menghadap sisi AB dan menghadap sisi PQ.
Maka
Contoh 1 : Diketahui dua segitiga ΔKLM dan ΔTUV berikut sebangun,
Tentukan panjang sisi TV !
Jawab :
Dua segitiga tersebut diketahui sebangun maka dari gambar dapat kita lihat dan simpulkan bahwa tentunya sudut dan Begitu juga
Yang dihadapi adalah sisi LM = 10 cm dan yang dihadapi adalah UV= 8 cm,
Yang dihadapi adalah KM = 7 cm dan yang dihadapi adalah TV yang akan kita cari.
Peritungannya adalah :
.
Jadi TV=5,6 cm .
B. Segitiga dalam Segitiga
Saya tidak tahu harus memberi nama bagaimana jadi kutulis saja “segitiga dalam segitiga“, tapi yang kami maksud adalah :
Pertama :
Diketahui segitiga ΔABC dan di dalamnya ada segitiga ΔDEC dimana AB//DE (sejajar), maka ΔABC sebangun dengan ΔDEC seperti nampak pada gambar berikut :
Berdasarkan pada bagian Permulaan, kita peroleh :
atau
Atau sering digunakan gambar bantu seperti berikut untuk mengingat :
yang harus diingat adalah darimana menarik garis lengkung panah tersebut, yaitu harus dari titik sudut yang menghadap dua garis sisi sejajar.
Kedua
Diketahui segitiga ABC siku-siku di B, dan BD merupakan garis tinggi (sehingga BD tegak lurus dengan AC)
Kesimpulan :
Demikian penjelasan mengenai Kesebangunan Dua Segitiga, Kesimpulan yang dapat kita ambil dari pembelajaran kita hari ini adalah dua buah bangun datar dikatakan sebangun (similar) jika sisi-sisi yang bersesuaian mempunyai perbandingan yang sama. Khusus untu segitiga sebagai bangun datar poligon dengan jumlah sisi paling sedikit, asal dua buah segitiga sudut-sudutnya sama besar maka sudah sebangun.
Semoga dengan penjelasan dan contoh di atas , kalian akan bertambah ilmunya dan dapat memahami nya. Jika ada yang ingin ditanyakan silahkan isi kolom kometar di bawah ini..
Wassalamualaikum Warrohmatullahi Wabarrohkatuh..
Sumber :
https://www.antotunggal.com/2021/11/materi-kesebangunan-bangun-datar.html
https://www.pijarbelajar.id/blog/kekongruenan-dan-kesebangunan