TRANSFORMASI GEOMETRI 2

 Senin - Kamis, 29 - 30 November 2021

Guru            : Fara Dibah, S.Pd

Mapel          : Matematika

Kelas           : IX E, F, G

 

Kode KD     : 

3.5 Menjelaskan transformasi geometri (refleksi , translasi, rotasi, dan dilatasi)

4.5 Menyelesaikan masalah konstektual yang berkaitan dengan transformasi

Menganalisis 

Materi          : Transformasi Giometri

Tujuan          : 

1. Peserta didik dapat menyimpulkan pengertian dari transformasi geometri (refleksi , translasi)

2. Peserta didik dapat menyelesaikan masalah konstektual yang berkaitan dengan transformasi

Assalamualaikum Warromatullahi Wabarrohkatuh..

Selamat pagi Semua !

Bagaimana Kabar Soleh/Soleha hari ini ?…

Semoga kita semua dalam lindungan Allah SWT. Aamiin ..

Baiklah Soleh/Soleha, Pertemuan hari ini kita akan memasuki materi baru . Silahkan di simak materi ibu berikut ini :

Transformasi Geometri

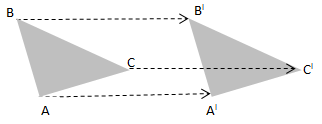
Transformasi geometri merupakan perubahan suatu bidang geometri yang meliputi posisi, besar dan bentuknya sendiri. Jika hasil transformasi kongruen dengan bangunan yang ditranformasikan, maka disebut transformasi isometri. Transformasi isometri sendiri memiliki dua jenisya itu transformasi isometri langsung dan transformasi isometri berhadapan. Transformasi isometri langsung termasuk translasi dan rotasi, sedangkan transformasi isometri berhadapan termasuk refleksi.

Rotasi

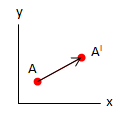
Rotasi atau perputaran merupakan transformasi geometri berupa pergeseran atau pemindahan semua titik pada bidang geometri sepanjang busur lingkaran yang memiliki titik pusat lingkaran sebagai titik rotasi. Rotasi dinyatakan positif jika arahnya berlawanan jarum jam, dan bernilai negatif jika searah jarum jam. Sebagai contoh:

Titik A berotasi 90o berlawanan arah jarum jam. Dalam diagram cartesius, bentuk-bentuk rotasi sebagai berikut:

Dilatasi

Dilatasi merupakan transformasi geometri berupa perkalian yang memperbesar atau memperkecil suatu bangunan geometri. Dalam konsep dilatasi, ada yang disebut titik dilatasi dan faktor dilatasi.

Titik dilatasi merupakan titik yang menentukan posisi suatu dilatasi. Titik dilatasi menjadi titik pertemuan dari semua garis lurus menghubungkan antara titik-titik dalam suatu bangun ketitik-titik hasil dilatasi.

Faktor dilatasi merupakan faktor perkalian suatu bangun geometri yang didilatasikan. Faktor ini menunjukan seberapa besar hasil dilatasi terhadap bangun geometrinya dan dinotasikan dengan k. Nilai k > 1 atau k < -1 menunjukan hasil dilatasi lebih besar dari geometrinya. Nilai -1 < k < 1 menunjukan hasil dilatasi lebih kecil dari geometrinya. Tanda positif mengartikan geometri dan hasil dilatasi berdampingan di salah satu sisi titik dilatasi. Sedangkan tanda negatif mengartikan geometri dan hasil dilatasi saling terbalik dan berlainan sisi di titik dilatasi.

Dilatasi dapat ditulis:

(D, k) = (Titik dilatasi, faktor dilatasi)

Konsep dilatasinya:

Faktor Dilatasi	Bentuk Dilatasi
k > 1
0 < k < 1
k < -1
-1 < k < 0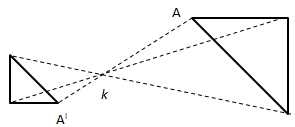

Dengan ketentuan:

• k adalah titik dilatasi
• A salah satu titik geometri
• AI hasil dilatasi titik A

Dalam diagram cartesius, bentuk-bentuk rotasi sebagai berikut:

Tetap semangat dan Wassalamualaikum..

TRANSFORMASI GEOMETRI 1

 Senin - Kamis, 15 - 17 November 2021

Guru            : Fara Dibah, S.Pd

Mapel          : Matematika

Kelas           : IX E, F, G

 

Kode KD     : 

3.5 Menjelaskan transformasi geometri (refleksi , translasi, rotasi, dan dilatasi)

4.5 Menyelesaikan masalah konstektual yang berkaitan dengan transformasi

Menganalisis 

Materi          : Transformasi Giometri

Tujuan          : 

1. Peserta didik dapat menyimpulkan pengertian dari transformasi geometri (refleksi , translasi)

2. Peserta didik dapat menyelesaikan masalah konstektual yang berkaitan dengan transformasi

Assalamualaikum Warromatullahi Wabarrohkatuh..

Selamat pagi Semua !

Bagaimana Kabar Soleh/Soleha hari ini ?…

Semoga kita semua dalam lindungan Allah SWT. Aamiin ..

Baiklah Soleh/Soleha, Pertemuan hari ini kita akan memasuki materi baru . Silahkan di simak materi ibu berikut ini :

Transformasi Geometri

Transformasi geometri merupakan perubahan suatu bidang geometri yang meliputi posisi, besar dan bentuknya sendiri. Jika hasil transformasi kongruen dengan bangunan yang ditranformasikan, maka disebut transformasi isometri. Transformasi isometri sendiri memiliki dua jenisya itu transformasi isometri langsung dan transformasi isometri berhadapan. Transformasi isometri langsung termasuk translasi dan rotasi, sedangkan transformasi isometri berhadapan termasuk refleksi.

Refleksi

Refleksi merupakan transformasi geometri berupa pergeseran atau pemindahan semua titik pada bidang geometri kearah sebuah garis atau cermin dengan jarak sama dengan dua kali jarak titik kecermin. Ada dua sifat penting dalam refleksi:

• Jarak titik kecermin sama dengan jarak bayangan titik ke cermin.
• Geometri yang direfleksikan berhadapan dengan petanya.

Sebagai contoh:

Bentuk refleksi terhadap berbagai garis sebagai berikut:

Titik		Garis/Kurva		Gambar Refleksi
Awal	Bayangan	Awal	Bayangan
Refleksi sumbu y
A(x, y)	AI (-x, y)	y = f(x)	yI = f(-x)
Refleksi sumbu y = h
A(x, y)	AI (x, 2h – y)	y = f(x)	yI = 2h – f(x)
Refleksi sumbu x = h
A(x, y)	AI (2h – x, y)	y = f(x)	yI = f(2h – x)
Refleksi sumbu y = x
A(x, y)	AI (y, x)	y = f(x)	x = f(y)
Refleksi sumbu y = -x
A(x, y)	AI (-y, -x)	y = f(x)	x = -f(-y)
Refleksi terhadap titik O (0,0)
A(x, y)	AI (-x, -y)	y = f(x)	yI = -f(-x)

Selain refleksi terhadap garis diatas, titik dan kurva juga dapat direfleksikan terhadap suatu garis y=mx+k. Berikut refleksinya:

Dapat di gambarkan:

Translasi

Translasi merupakan pergeseran atau pemindahan semua titik pada bidang geometri sejauh dan arah yang sama. Penulisan atau notasi translasi sama dengan notasi vektor. Jika titik B ditranslasi sampai titik  maka dapat dinotasikan:

Sebagai contoh:

Titik A, B, dan C, masing-masing ditranslasikan ke titik AI, BI, dan CI dengan jarak dan arah yang sama.

Suatu translasi dapat ditinjau terhadap sumbu x dan sumbu y. Pergeseran sejauh a sejajar sumbu x (bergeser ke kanan a>0, ke kiri a<0) dan pergeseran sejauh b sejajar sumbu y (bergeser ke atas b>0, ke bawah b<0) dinyatakan sebagai:

Dengan a dan b adalah komponen translasi. Bentuk-bentuk translasi sejauh sebagai berikut:

Posisi Awal	Posisi Akhir	Pergeseran
Translasi Titik
A(x, y)	AI (x+a, y+b) Dengan x dan y adalah koordinat
Translasi Garis
mx+ny=c	m(x + a) + n(y + b) = c Dengan m dan n adalah koefisien dan c konstanta
Translasi Kurva
y = mx2+ kx + l	Dengan m dan k adalah koefisien dan l konstanta
Translasi Lingkaran
x2 + y2 = c	Dengan c adalah konstanta

setelah kalian menyimak materi di atas, silahkan kalian buka buku cetak HIJAU halaman 135 ada TUGAS RUMAH. Kerjakan dibuku latihan dan kirim melalui email ibu dibafara0220@gmail.com paling lambat Jumat 19 November 2021.

Tetap Semangat..

Wassalamualaikum Warromatullahi Wabarrohkatuh..

MENYUSUN RUMUS FUNGSI KUADRAT

  Senin - Kamis, 08 - 10 November 2021

Guru            : Fara Dibah, S.Pd

Mapel          : Matematika

Kelas           : IX E, F, G

 

Kode KD     :

Menganalisis Sumbu Simetri dan Nilai Optimum Grafik Fungsi Kuadrat

Materi          : Fungsi Kuadrat

Tujuan          : 

1. Peserta didik dapat menyimpulkan pengertian dari sumbu simetri serta nilai optimum suatu grafik fungsi dengan tepat.

2. Peserta didik dapat menerapkan rumus persamaan sumbu simetri dan nilai optimum untuk menyelesaikan masalah nyata secara tepat.

Assalamualaikum Warromatullahi Wabarrohkatuh..

Selamat pagi Semua !

Bagaimana Kabar Soleh/Soleha hari ini ?…

Semoga kita semua dalam lindungan Allah SWT. Aamiin ..

Soleh/Soleha dipertemuan sebelumnya kalian sudah menyimak materi yang ada divideo blogger ibu seperti ini :

setelah kalian menyimak materi sebelumnya, maka silahkan kalian buka Buku Hijau Halaman 80 Kegiatan 3.3 

Langkah-Langkah Pembelajaran :

1. Buka Buku Hijau Halaman 80 Kegiatan 3.3 atau lihat gambar dibawah ini.

2. Kerjakan dikertas Folio 

3. Diskusikan bersama teman mu

4. Kegiatan tersebut dikumpul saat pertemuan Pembelajaran Tatap Muka dipertemuan selanjutnya.

Tetap semangat dan Wassalamualaikum..