MATEMATIKA
BILANGAN BENTUK AKAR
PERTEMUAN KE 5
IDENTITAS
Hari, tanggal : Senin, 5 Agustus 2024
Kelas : IX C dan IX D
Guru Mapel : Fara Dibah, S.Pd
Kode KD :
3.1 Menjelaskan dan melakukan operasi bilangan berpangkat, bilangan rasional dan bentuk akar, serta sifat-sifatnya.
4.1 Menyelesaikan masalah yang berkaitan dengan sifat-sifat operasi bilangan berpangkat bulat dan bentuk akar.
Materi : Bilangan Bentuk Akar
Tujuan : Peserta didik dapat mengenal dan menyelesaikan operasi Bilangan Bentuk Akar
Mengenal Bentuk Akar
Bentuk akar adalah akar dari suatu bilangan rasional yang hasilnya berupa bilangan irasional.21/2 (a = 2, m = 1, n = 2)
21/2 = ![]() atau √2
atau √2
kalo indeks akarnya bernilai 2, nggak perlu kamu tulis juga nggak papa, ya.
Contoh bentuk akar yang lain di antaranya √6, √7, √11, 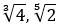 dan
masih banyak lagi. Coba aku tanya, √25 itu termasuk bentuk akar atau
bukan, sih? Eits! Jawabannya bukan bentuk akar. Kenapa? Ingat
definisinya, bentuk akar itu berupa bilangan irasional, sedangkan √25
bisa kita sederhanakan menjadi √52 = 52/2 = 5 (5 adalah bilangan rasional). Jadi, √25 bukan bentuk akar. Paham, ya?
dan
masih banyak lagi. Coba aku tanya, √25 itu termasuk bentuk akar atau
bukan, sih? Eits! Jawabannya bukan bentuk akar. Kenapa? Ingat
definisinya, bentuk akar itu berupa bilangan irasional, sedangkan √25
bisa kita sederhanakan menjadi √52 = 52/2 = 5 (5 adalah bilangan rasional). Jadi, √25 bukan bentuk akar. Paham, ya?
Sifat-Sifat Bentuk Akar
Seperti halnya bilangan berpangkat, bilangan bentuk akar juga memiliki sifat-sifat tertentu, lho! Sifat-sifat ini akan memudahkan kita dalam melakukan operasi aljabar yang melibatkan bentuk akar nantinya. Sifat-sifat bentuk akar, di antaranya sebagai berikut:

Operasi Bentuk Akar
Sama seperti bilangan bulat, bentuk akar juga bisa dioperasikan baik dengan bentuk akar lain maupun dengan bilangan real. Adapun operasinya adalah sebagai berikut.
1. Penjumlahan
Penjumlahan hanya bisa dilakukan jika angka yang berada di dalam tanda akar nilainya sama. Bentuk penjumlahannya adalah sebagai berikut.
p√x + q√x = (p+q)√x
Contoh:
- √2 + √2 = (1+1)√2=2√2
- 2√5 +3√5 = (2+3)√5=5√5
Penjumlahan tidak bisa dilakukan pada:
- Bentuk akar dan bilangan bulat biasa, misalnya, √2 + 2 ; dan
- Antarbentuk akar yang tidak sama bilangan pokoknya, misalnya√2 + √3.
2. Pengurangan
Konsep pengurangan sama seperti penjumlahan, yaitu hanya bisa dilakukan pada dua bentuk akar atau lebih yang bilangan pokoknya sama. Bentuk pengurangannya adalah sebagai berikut.
p√x – q√x = (p-q)√x
Contoh:
- 2√2 – √2 = (2-1)√2 = √2
- 2√5 – 3√5 = (2-3)√5 = –√5
3. Perkalian
Konsep perkalian bentuk ini berbeda dengan penjumlahan dan pengurangan. Hal itu karena perkalian bisa dilakukan antara bentuk akar dan bilangan nonakar, baik pecahan maupun bilangan bulat. Bentuk perkaliannya adalah sebagai berikut.
- p√x × q = (p×q)√x
- p√x × q√y = (p×q)√xy
Contoh perkaliannya adalah sebagai berikut.
- 4√7 × 2 = (4×2)√7 = 8√7
- √3 × 2√11 = (1×2)√33 = 2√33
3. Pembagian
Konsep pembagian, hampir sama dengan perkalian. Namun, pembagian bisa menghasilkan pecahan yang penyebutnya memuat bentuk akar. Jika berbentuk demikian, maka pecahan harus dirasionalkan penyebutnya. Adapun bentuk pembagiannya adalah sebagai berikut.
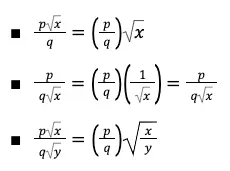
Contoh:
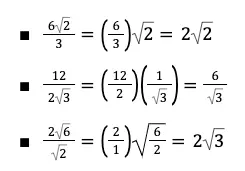


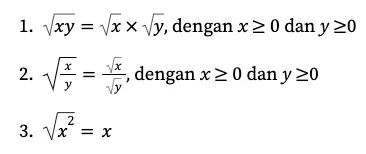

Tidak ada komentar:
Posting Komentar