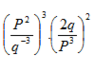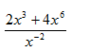IDENTITAS
Mata Pelajaran : Matematika
Kelas : IX C dan IX D
Pertemuan : -
Materi : Bilangan Berpangkat & Bentuk Akar dan Persamaan Kuadrat
Guru Pengampu : Fara Dibah, S.Pd
Waktu Pembelajaran: Rabu, 2 Oktober 2024
Kompetensi Dasar :
3.1 Menjelaskan dan melakukan operasi bilangan berpangkat, bilangan rasional dan bentuk akar, serta sifat-sifatnya.
4.1 Menyelesaikan masalah yang berkaitan dengan sifat-sifat operasi bilangan berpangkat bulat dan bentuk akar.
3.2 Menjelaskan persamaan kuadrat dan karakteristiknya berdasarkan akar-akarnya serta cara penyelesaiannya
4.2 Menyelesaikan masalah yang berkaitan dengan persamaan kuadrat.
TUJUAN PEMBELAJARAN :
Setelah
mengikuti pembelajaran, Peserta didik dapat menjawab Soal Penilaian Tengah Semester (PTS) ganjil dengan materi Bilangan Berpangkat & Bentuk Akar dan Persamaan Kuadrat
Dalam pembagian bilangan berpangkat berlaku rumus :
Operasi Bilangan Bentuk Akar
Sama seperti bilangan bulat, bentuk akar juga bisa dioperasikan baik dengan bentuk akar lain maupun dengan bilangan real. Adapun operasinya adalah sebagai berikut.
1. Penjumlahan
Penjumlahan hanya bisa dilakukan jika angka yang berada di dalam tanda akar nilainya sama. Bentuk penjumlahannya adalah sebagai berikut.
p√x + q√x = (p+q)√x
Contoh:
- √2 + √2 = (1+1)√2=2√2
- 2√5 +3√5 = (2+3)√5=5√5
Penjumlahan tidak bisa dilakukan pada:
- Bentuk akar dan bilangan bulat biasa, misalnya, √2 + 2 ; dan
- Antarbentuk akar yang tidak sama bilangan pokoknya, misalnya√2 + √3.
2. Pengurangan
Konsep pengurangan sama seperti penjumlahan, yaitu hanya bisa dilakukan pada dua bentuk akar atau lebih yang bilangan pokoknya sama. Bentuk pengurangannya adalah sebagai berikut.
p√x – q√x = (p-q)√x
Contoh:
- 2√2 – √2 = (2-1)√2 = √2
- 2√5 – 3√5 = (2-3)√5 = –√5
3. Perkalian
Konsep perkalian bentuk ini berbeda dengan penjumlahan dan pengurangan. Hal itu karena perkalian bisa dilakukan antara bentuk akar dan bilangan nonakar, baik pecahan maupun bilangan bulat. Bentuk perkaliannya adalah sebagai berikut.
- p√x × q = (p×q)√x
- p√x × q√y = (p×q)√xy
Contoh perkaliannya adalah sebagai berikut.
- 4√7 × 2 = (4×2)√7 = 8√7
- √3 × 2√11 = (1×2)√33 = 2√33
3. Pembagian
Konsep pembagian, hampir sama dengan perkalian. Namun, pembagian bisa menghasilkan pecahan yang penyebutnya memuat bentuk akar. Jika berbentuk demikian, maka pecahan harus dirasionalkan penyebutnya. Adapun bentuk pembagiannya adalah sebagai berikut.
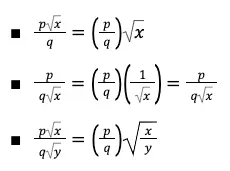
Contoh:
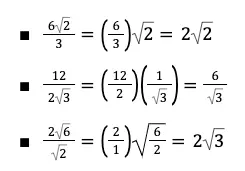
Persamaan Kuadrat
Persamaan kuadrat adalah persamaan polinomial (suku banyak) variabel 1 yang memiliki pangkat tertinggi dua. Ingat, ya, pangkat tertingginya dua! Jadi, kalau kamu nyariin pangkat tiga di persamaan kuadrat, ya kagak bakalan ketemu, yak.
Nah, bentuk umum persamaan kuadrat bisa dituliskan seperti berikut:
ax2 + bx + c = 0
Dengan a, b, c ∈ R dan a ≠ 0
Keterangan:
x = variabel
a = koefisien dari x2
b = koefisien dari x
c = konstanta
Dalam mempelajari persamaan kuadrat, tentunya kamu nggak akan terlepas dari yang namanya menyelesaikan persamaan kuadrat. Hmm, menyelesaikan tuh, maksudnya gimana sih? Emangnya persamaan kuadrat punya masalah, kok harus diselesaiin segala?
Tentu punya, dong! Masalah yang dimiliki persamaan kuadrat terletak pada nilai x-nya.
Jadi, seperti yang udah kita tau dari bentuk umumnya, persamaan kuadrat itu punya variabel x yang nggak diketahui nilainya berapa. Nah, nilai x inilah yang mau kita cari! Cara mencari nilai x adalah dengan menyelesaikan persamaan kuadrat tersebut.
Terus, cara menyelesaikan persamaan kuadrat kaya gimana, kak?
Cara Menyelesaikan Persamaan Kuadrat
Ada tiga cara untuk menyelesaikan persamaan kuadrat, yaitu dengan menggunakan faktorisasi, kuadrat sempurna, dan rumus kuadratik atau biasa disebut juga sebagai rumus ABC. Kita bahas satu per satu, ya!
1. Faktorisasi
Faktorisasi atau pemfaktoran merupakan cara mencari penyelesaian dari persamaan kuadrat, dengan cara mencari nilai yang jika dikalikan, maka akan menghasilkan nilai lain.
Ada tiga bentuk persamaan kuadrat dengan faktorisasi yang berbeda, yakni seperti berikut:
| No. | Persamaan Kuadrat | Faktorisasi |
| 1 | x2 + 2xy + y2 = 0 | (x + y)2 = 0 |
| 2 | x2 − 2xy + y2 = 0 | (x − y)2 = 0 |
| 3 | x2 − y2 = 0 | (x + y)(x − y) = 0 |
Dengan x = variabel dan y = konstanta
Next, coba kita kerjakan contoh soal di bawah ini, ya!
Contoh Soal Faktorisasi
Selesaikan persamaan kuadrat berikut dengan cara faktorisasi 5x2 + 13x + 6 = 0!
Jawab:
5x2 + 13x + 6 = 0
5x2 + 10x + 3x + 6 = 0
5x(x + 2) + 3(x + 2) = 0
(5x + 3)(x + 2) = 0
5x = −3
x = ![]() atau x = −2
atau x = −2
Jadi, penyelesaiannya adalah x = ![]() atau x = −2.
atau x = −2.
2. Melengkapi Kuadrat Sempurna
Bentuk ax2 + bx + c = 0 bisa kamu jabarkan menjadi seperti berikut.
(x + p)2 = q
Perhatikan contoh berikut.
Bentuk persamaan kuadrat: x2 + 5x + 6 = 0
x2 + 8x + 6 = 0
(x2 + 8x) = -6
x2 + 8x +16 = -6 +16
(x + 4)2 = 10
(x + 4) = ± √10
x = √10 – 4 atau x = -√10 – 4
3. Rumus ABS
Rumus abc merupakan alternatif pilihan ketika persamaan kuadrat sudah tidak bisa diselesaikan dengan metode faktorisasi maupun kuadrat sempurna.
Berikut rumus formula abc pada persamaan kuadrat ax2 +bx + c = 0.

Berikut contoh penyelesaian soal persamaan kudrat menggunakan formula abc.
Selesaikan persamaan x2 + 4x – 12 = 0 menggunakan metode formula abc!
Penyelesaian:
x2 + 4x – 12 = 0
dengan a=1, b=4, c=-12

Dan agar kalian lebih memahami lagi tentang mencari akar-akar persamaan kuadrat, maka silahkan kalian simak video berikut :