IDENTITAS
Mata Pelajaran : Matematika
Kelas : IX C dan IX D
Pertemuan : Ke 3
Materi : Nilai dan Grafik Fungsi Kuadrat
Guru Pengampu : Fara Dibah, S.Pd
Waktu Pembelajaran: Rabu, 30 Oktober 2024
Alat Peraga : Buku Berpetak, Pensil, Penggaris
Media Pembelajaran : LCD Proyektor dan Laptop
Kompetensi Dasar :
3.3 Menjelaskan fungsi kuadrat dengan menggunakan tabel, persamaan , dan grafik
4.3 Menyajikan fungsi kuadrat menggunakan tabel, persamaan, dan grafik
TUJUAN PEMBELAJARAN :
Setelah
mengikuti pembelajaran, Peserta didik dapat menentukan nilai
fungsi kuadrat dan menggambarkannya dalam bentuk grafik fungsi kuadrat.
Apakah kalian masih ingat bagaimana bentuk persamaan kuadrat? Bentuknya seperti ini, guys, ax² + bx + c = 0. Nah, kalau bentuk umum fungsi kuadrat bagaimana? Hanya berbeda sedikit saja. Perhatikan di bawah ini.
f(x) = ax² + bx + c
f(x) = fungsi kuadrat
x = variabel
a, b = koefisien
c = konstanta
a ≠ 0
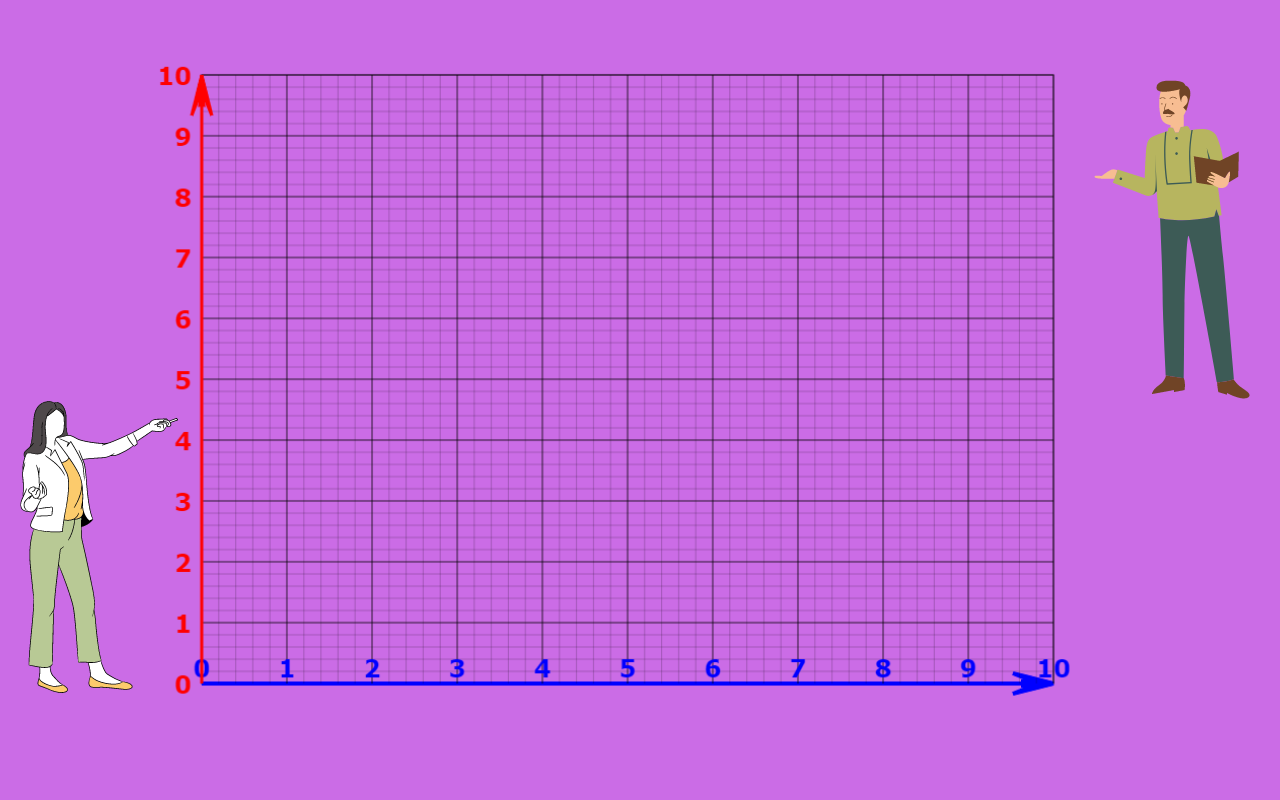
Pada submateri ini, kita akan membahas tentang bagaimana bentuk-bentuk dari fungsi kuadrat. Langsung saja, nak. Misal kita punya fungsi kuadrat y = x² dan ingin menggambar fungsi tersebut, kita akan membuat tabelnya terlebih dahulu.
Kita ambil contoh nilai-nilainya seperti pada contoh di bawah ini. Kemudian, tandai titik-titik potongnya dan kita dapati grafik fungsi kuadratnya. Catatan yang perlu diketahui kalian, garis pada grafik tidak boleh tegak lurus karena akan membedakan nilai-nilai yang memenuhinya.
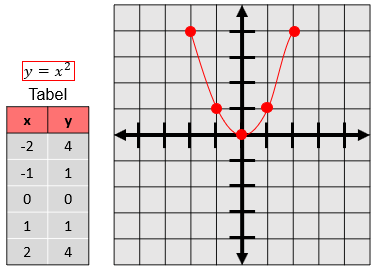
Sebelumnya kita sudah lihat grafik berdasarkan tabel, sekarang kita akan melihat grafik dari persamaan. Persamaan akan memudahkan menggambar titik potong x dan y.
Misalnya, kita punya persamaan y = x² + 2x +1, kita cari titik potong terhadap sumbunya.
Titik potong terhadap sumbu y
x = 0
y = 0² + 2(0) +1
y = 1
Titik potong (0, 1)
Titik potong terhadap sumbu x
x² + 2x +1 = 0
(x + 1)(x + 1) = 0
x = -1
Titik potong (-1, 0)
Setelah mengetahui nialinya, kita coba gambar grafiknya.
Hubungan antara Koefisien dengan Grafik Fungsi Kuadrat
Lanjut ke pembahasan selanjutnya yaitu mengenai materi grafik fungsi kuadrat dan hubungannya dengan koefisien.
Kita akan mencari tahu hubungan antara koefisien (a, b, dan c) dengan grafik.
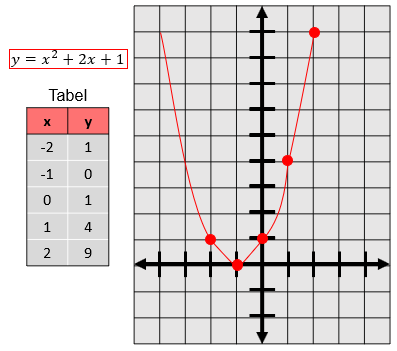
Koefisien A
Langsung kita bahas koefisien a atau koefisien kuadrat. Misalnya kita punya y = x² + 1, y = -x² + 1, dan y = ½ x² + 1, maka grafiknya akan seperti pada berikut.
Kesimpulannya:
Jika a > 0, grafik terbuka ke atas
Jika a < 0, grafik terbuka ke bawah
Semakin besar nilai a, bentuk grafik semakin sempit
Koefisien B
Pada materi ini, diperlukan pengetahuan kalian tentang melengkapkan kuadrat sempurna, ya.
Koefisien B disebut juga koefisien linear. Langsung saja, misalnya kita punya contoh persamaan y = x² + 2x + 4.
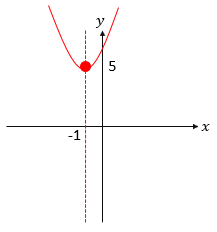
Kemudian, bentuk tersebut jika dilengkapi kuadrat sempurnanya akan menjadi (x + 1)² + 5, selanjutnya 1 kita sebut c dan 5 kita sebut d. Sebelumnya perlu elo ketahui dulu tentang ini.
Jika c positif, maka sumbu simetri x = -c, titik puncak (-c, d)
Jika c negatif, maka sumbu simetri x = c, titik puncak (c, d)
Kira-kira, grafiknya akan seperti berikut.
Konstanta C
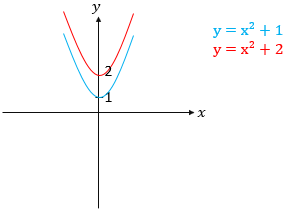
Sekarang, kita bahas konstanta c terhadap grafik fungsi kuadrat. Konstanta c berpengaruh pada titik potong sumbu y.
Jika c semakin besar, semakin berada di atas
Jika c semakin kecil, semakin berada di bawah
Perhatikan grafik di bawah
Soal 1
Jika f(x) = x² – 4x, berapakah nilai dari f(2)?
Jawab:
f(2) = 2² – 4(2) = 4 – 8 = -4
Fungsi kuadrat yang memotong sumbu x di titik (3, 0) dan (-3, 0) melalui titik (0, -9) adalah …
Jawab
y = a(x – x₁)(x – x₂)
y = a(x + 3)(x – 3)
melalui titik (0, -9)
-9 = a(0 + 3)(0 – 3)
-9 = -9a
a = 1
y = 1(x + 3)(x – 3)
y = -9 + x²
Jadi, fungsi kuadrat tersebut adalah y = -9 + x².
Itu dia penjelasan singkat mengenai materi fungsi kuadrat dan grafiknya beserta contoh soal dan rumus-rumus dalam menyelesaikannya.

