Senin - Kamis, 13 - 16 September 2021
Guru : Fara Dibah, S.Pd
Mapel : Matematika
Kelas : IX E, F, G
Kode KD :
3.2 Menjelaskan persamaan kuadrat dan karakteristiknya berdasarkan akar-akarnya serta cara penyelesaiannya.
4.2 Menyelesaikan masalah yang berkaitan dengan akar-akar persamaan kuadrat.
Materi : Akar-Akar Persamaan Kuadrat
Tujuan :
1. Peserta didik dapat menjelaskan persamaan kuadrat dan karakteristiknya berdasarkan akar-akarnya serta cara penyelesaiannya.
2. Peserta didik mampu menyelesaikan masalah yang berkaitan dengan akar-akar persamaan kuadrat.
Mencari Akar-akar Persamaan Kuadrat
Ada tiga cara untuk mencari akar-akar dalam menyelesaikan persamaan kuadrat, yaitu dengan faktorisasi, kuadrat sempurna dan dengan menggunakan rumus abc.
1. Faktorisasi
Faktorisasi atau pemfaktoran merupakan cara mencari akar-akar persamaan kuadrat dengan mencari nilai yang jika dikalikan akan menghasilkan nilai lain. Ada tiga bentuk persamaan kuadrat dengan faktorisasi akar-akar yang berbeda seperti berikut:

Selanjutnya, coba kita kerjakan contoh soal di bawah ini:
Selesaikan persamaan kuadrat berikut dengan cara faktorisasi 5x2+13x+6=0
Jawab:

2. Kuadrat Sempurna
Tidak semua persamaan kuadrat bisa diselesaikan dengan cara faktorisasi, cara lain untuk menyelesaikan persamaan kuadrat dengan cara melengkapkan kuadrat sempurna. Bentuk persamaan kuadrat sempurna adalah bentuk persamaan yang menghasilkan bilangan rasional. Penyelesaian persamaan kuadrat dengan melengkapkan kuadrat menggunakan rumus:
(x+p)2 = x2 + 2px + p2
Ubah menjadi bentuk persamaan dalam (x+p)2 = q
Penyelesaian:
(x+p)2 = q
x+p = ± q
x = -p ± q
Supaya kamu lebih paham, coba kerjakan contoh soal melengkapi bentuk kuadrat sempurna di bawah ini:
x2 + 6x + 5 = 0
Jawab:
x2 + 6x +5 = 0
Ubah menjadi x2 + 6x = -5
Tambahkan satu angka di ruas kiri dan kanan agar menjadi kuadrat sempurna. Penambahan angka ini diambil dari separuh angka koefisien dari x atau separuhnya 6 yang dikuadratkan, yakni 32=9. Tambahkan angka 9 di ruas kiri dan kanan, sehingga persamaannya menjadi:
x2 + 6x + 9 = -5 + 9
x2 + 6x + 9 = 4
(x+3)2 = 4
(x+3) = √4
x = 3 ± 2
- Untuk x+3 = 2
x = 2-3
x = -1
- Untuk x+3 = -2
x = -2-3
x = -5
Jadi, x= -1 atau x = -5
3. Rumus Kuadrat
Selain menggunakan faktorisasi dan dengan melengkapi kuadrat sempurna, persamaan kuadrat dapat diselesaikan dengan menggunakan rumus kuadrat atau biasa dikenal dengan rumus abc.

Selanjutnya, coba kerjakan contoh soal berikut menggunakan rumus abc!
x2 + 4x - 12 = 0
Jawab:
x2 + 4x - 12 = 0
a=1, b=4, c=-12

terimakasih soleh/soleha, demikian pembelajaran hari ini. Bagi yang ingin bertanya silahkan isi kolom komentar di bawah ini atau WA ibu via japri. Dan untuk kegiatan interaktif kita hari ini akan kita laksanakan di siang hari ini mulai pukul 13.00 WIB. Untuk tugas hari ini akan ibu share di WA .
Semangat yang belajar di Sekolah dan Tetap semangat juga yang belajar online dari rumah.
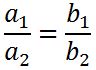
assalamualaikum bu, terimakasih atas materinya
BalasHapusAnnika 9E
Assalamualaikum bu terimakasih
BalasHapusAzman 9E
Assalamualaikum bu terimakasih
BalasHapusFaiz 9E
terimakasi mam atas materinya
BalasHapus-M.athalla putra
9E
terimakasi mam atas materinya
BalasHapus-M.Davie M
9E
assalamualaikum bu, terimakasih atas materinya
BalasHapus-arga Irawan 9e
Assalamualaikum bu,terimakasih atas materinya
BalasHapusaurelia damayanti 9e
assalamualaikum terimakasih bu - cut ajirna Afifah azahra 9E
BalasHapusAssalamualaikum mam terimakasih
BalasHapusAlfi 9E
Assalamualaikum bu,terimakasih atas materinya
BalasHapusRidho Tri Islando 9E
Assalamualaikum Bu terimakasih tugasnya
BalasHapusAulia Putri 9f hady
~Irsyad 9E
BalasHapusTerimakasih atas materinya Mam
✦⸱࣭👘𖥻.˚ ࣪Assalamualaikum bu terima kasih atas materinya ♡ : 交 !!
BalasHapus!さ؛.⊹Pruezalya Ramadhani Wijaya 9F ❪🎏❫
assalamualaikum, terimakasih bu
BalasHapusdera 9f