BRSL KERUCUT & BOLA

MATA PELAJARAN : MATEMATIKA

WAKTU PEMBELAJARAN :

KELAS IX D, E, F : 01 - 02 MARET 2023


KOMPETENSI DASAR :

3.7       Membuat generalisasi luas permukaan dan volume berbagai bangun ruang sisi lengkung (tabung, kerucut, dan bola)

 4.7     Menyelesaikan masalah kontekstual yang berkaitan dengan luas permukaan dan volume bangun ruang sisi lengkung (tabung, kerucut, dan bola), serta gabungan beberapa bangun ruang sisi lengkung

 

TUJUAN PEMBELAJARAN :

Setelah mengikuti pembelajaran, Peserta didik diharapkan dapat :
1.  Mengidentifikasi unsur-unsur bangun ruang sisi lengkung (kerucut dan bola) melalui gambar, video atau benda nyata

2.  Mengidentifikasi bentuk dan ukuran sisi jaring-jaring kerucut, dan bola

3.  Membuat generalisasi luas permukaan dan volume bangun ruang sisi lengkung kerucut

4.  Membuat generalisasi luas permukaan dan volume bangun ruang sisi lengkung bola



MATERI PEMBELAJARAN :

Pengertian bangun ruang sisi lengkung

Bangun ruang sisi lengkung adalah suatu kelompok bangun ruang yang memiliki sisi melengkung, memiliki selimut atau memiliki permukaan bidang. Seperti yang telah saya beri tahu di atas tadi, bahwa kelompok bangun ruang yang memiliki sisi lengkung adalah meliputi bola, kerucut dan tabung.

 

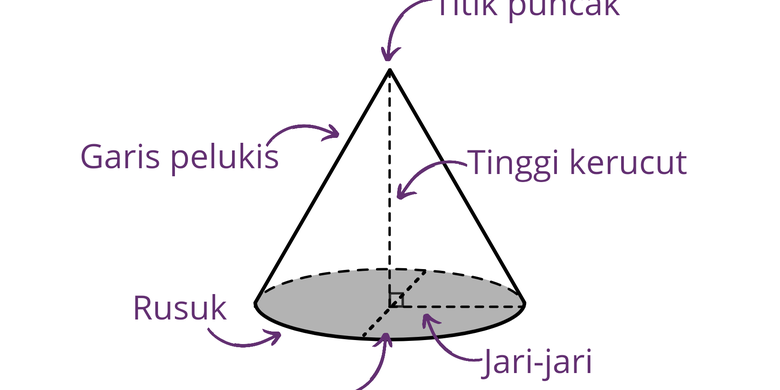
Kerucut

Kerucut merupakan bangun ruang yang memiliki alas berbentuk lingkaran dimana lingkaran tersebut tutupi oleh selimut yang memiliki ketinggian sejumlah t. Selimut tersebut diseut garis pelukis. Unsur – unsur yang terdapat pada kerucut adalah:

(r) = jari – jari lingkaran
(t) = tinggi kerucut
(s) = garis pelukis kerucut

 RUMUS LUAS PERMUKAAN DAN VOLUME KERUCUT :

 Luas Permukaan Kerucut:

 L = Luas Lingkaran + Luas Juring ABC

L  = πr2 + πrs

L  = πr(r + s)

 

 Volume Kerucut:

V = 1/3 La × t 

V = 1/3 πr2 × t

 

Contoh Soal :

Diberikan sebuah kerucut yang memiliki jari-jari sebesar r = 30 cm dan garis pelukis s = 50 cm seperti gambar berikut.

Tentukan:
a) tinggi kerucut
b) volume kerucut
c) luas selimut kerucut
d) luas permukaan kerucut

Pembahasan :
a) tinggi kerucut
Tinggi kerucut dicari dengan dalil atau rumus phytagoras dimana
t2 = s2 − r2
t2 = 502 − 302
t2 = 1600
t = √1600 = 40 cm

b) volume kerucut
V = 1/3 π r2 t
V = 1/3 x 3,14 x × 30 x 30 x 40
V = 37 680 cm3

c) luas selimut kerucut
L = π r s
L = 3,14 x 30 x 50
L = 4 710 cm2

d) luas permukaan kerucut L = π r (s + r)
L = 3,14 x 30 (50 + 30)
L = 3,14 x 30 x 80 = 7 536 2

Bola

 Bola merupakan salah satu bangun ruang yang memiliki sisi melengkung dimana terdapat jari – jari didalamnya. Pajang sisi 1 ke sisi yang lainnya disebut dengan diameter, atau bisa dikatakan panjang 2r = diameter. Unsur – unsur pada bola adalah:
(r) = jari – jari bola

 

RUMUS LUAS PERMUKAAN DAN VOLUME BOLA :

 Luas Permukaan Bola: L = 4πr2

Volume Bola: V = 4/3πr3

 

Contoh Soal :

Diberikan sebuah bola yang memiliki jari-jari sebesar 30 cm seperti gambar berikut.

Tentukan:

a) volume bola
b) luas permukaan bola

Pembahasan :
a) volume bola
V = 4/3 π r3
V = 4/3 x 3,14 x 30 x 30 x 30
V = 113 040 cm3

b) luas permukaan bola
L = 4π r2
L = 4 x 3,14 x 30 x 30
L = 11 304 cm2

Untuk Evaluasi kegiatan hari ini, silahkan kerjakan latihan 5.3 Pada buku Besar dengan memilih 5 soal secara diskusi ...