IDENTITAS
Mata Pelajaran : Matematika
Kelas : IX C dan IX D
Pertemuan : Ke 6
Materi : Hasil dan Jumlah Persamaan Kuadrat serta Membuat Persamaan Baru
Guru Pengampu : Fara Dibah, S.Pd
Waktu Pembelajaran: Rabu, 16 Oktober 2024
Alat Peraga : Buku Bergambar, Pensil, Penggaris
Media Pembelajaran : LCD Proyektor dan Laptop
Kompetensi Dasar :
3.2 Menjelaskan persamaan kuadrat dan karakteristiknya berdasarkan akar-akarnya serta cara penyelesaiannya
4.2 Menyelesaikan masalah yang berkaitan dengan persamaan kuadrat.
TUJUAN PEMBELAJARAN :
Setelah
mengikuti pembelajaran, Peserta didik dapat memahami dan menentukan hasil Jumlah dan Kali persamaan kuadrat serta dapat membuat Persamaan Kuadrat.
Menyusun Persamaan Kuadrat Baru
- Persamaan kuadrat awal adalah ax² + bx + c = 0
- Persamaan kuadrat baru adalah x² - (x1 + x2)x + x1 . x2 = 0
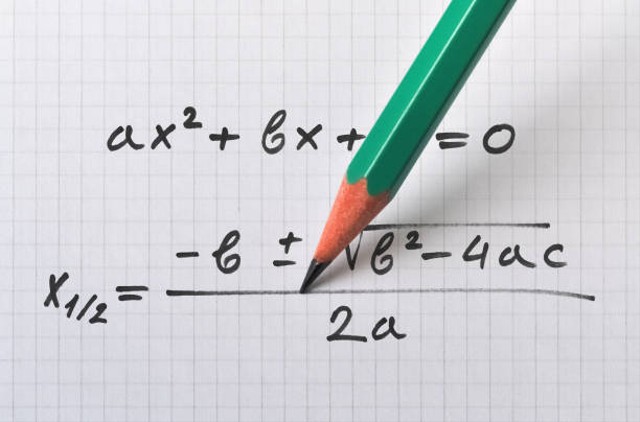
- Dengan cara menentukan jumlah dari hasil perkalian akar pada persamaan kuadrat awal.
- Dengan cara menentukan jumlah dan juga hasil perkalian pada akar-akar persamaan kuadrat baru yang telah diketahui.
- Dengan cara membentuk persamaan kuadrat baru yang sesuai rumus yang telah diberikan, yaitu x² - (x1 + x2)x + x1. x2 = 0 atau (x - x1) (x - x2) = 0.
Contoh Soal Persamaan Kuadrat Baru
1. Bentuk umum dari persamaan kuadrat x( x – 4 ) = 2x + 3 adalah
- x2 – 2x + 3 = 0
- x2 – 6x – 3 = 0
- 2x2 + 6x – 3 = 0
- x2 – 8x – 3 = 0
2.
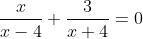
Nilai dari 2a + b – c adalah
- 21
- 19
- -15
- 8
3. Himpunan penyelesaian dari persamaan kuadrat 2x2 – x – 15 adalah
- {2, -3/2}
- {3,5}
- {3, -5/2}
- {3, -5/4}
4. Nilai diskriminan dari 4x2 – 2x + 1 = 0 adalah
- 12
- -15
- -12
- -14
5. Sita memiliki selembar kertas yang panjangnya (x +4) cm dan lebarnya (x – 2) cm. Jika luas kertas tersebut 40 cm2, nilai x adalah
- 10
- 8
- 6
- 4
Kesimpulan :
Untuk menyusun persamaan kuadrat baru, diperlukan rumus yang diperoleh dengan cara memanfaatkan rumus jumlah dan hasil kali akar persamaan kuadrat, yaitu sebagai berikut.
- Persamaan kuadrat awal adalah ax² + bx + c = 0
- Persamaan kuadrat baru adalah x² - (x1 + x2)x + x1 . x2 = 0
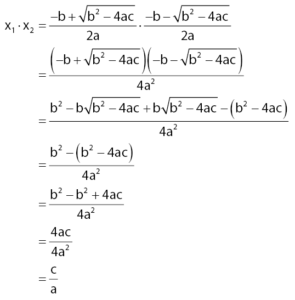


Tidak ada komentar:
Posting Komentar