Faradibaarifin: REFLEKSI DAN TRANSLASI

IDENTITAS

Mata Pelajaran : Matematika

Kelas : IX C dan IX D

Pertemuan : Ke 2

Materi : Transformasi Geometri (Refleksi dan Translasi)

Guru Pengampu : Fara Dibah, S.Pd

Waktu Pembelajaran: Senin, 13 Januari 2025

Alat Peraga : Buku Berpetak, Pensil, Penggaris

Media Pembelajaran : LCD Proyektor dan Laptop

Kompetensi Dasar :

3.4 Menjelaskan transformasi geometri (refleksi, translasi, rotasi, dan dilatasi) yang dihubungkan dengan masalah kontekstual

4.4 Menyelesaikan masalah kontekstual yang berkaitan dengan transformasi geometri (refleksi, translasi, rotasi, dan dilatasi

Materi : Mengidentifikasi masalah di sekitar yang melibatkan transformasi (refleksi, translasi)

Tujuan :

1. Peserta didik dapat mengidentifikasi masalah di sekitar yang melibatkan transformasi (refleksi, translasi)

2. Peserta didik dapat menggambar bentuk bangun atau titik koordinat yang melibatkan transformasi (refleksi, translasi)

Assalamualaikum Warromatullahi Wabarrohkatuh..

Selamat pagi Semua !

Bagaimana Kabar Soleh/Soleha hari ini ?…

Semoga kita semua dalam lindungan Allah SWT. Aamiin ..

Soleh/soleha apakah tadi subuh kalian sudah melaksanakan solat subuh tepat waktu ? untuk yang laki-laki solat subuh nya di masjid atau di musholla ya nak, agar kita mendapat keberkahan dari Allah SWT ..

Dan untuk yang perempuan silahkan solat subuh nya secara munfarid dirumah masing-masing..

Materi Pembelajaran :

Untuk pertemuan kedua di Semester Genap ini kita akan mempelajari tentang Salah satu materi Trasformasi Geometri yaitu Refleksi dan translasi, dan lebih jelas nya dalam memahami materi hari ini silahkan kalian baca dan pahami pembahasan materi berikut :

Refleksi

Refleksi merupakan transformasi geometri berupa pergeseran atau pemindahan semua titik pada bidang geometri kearah sebuah garis atau cermin dengan jarak sama dengan dua kali jarak titik kecermin. Ada dua sifat penting dalam refleksi:

Jarak titik kecermin sama dengan jarak bayangan titik ke cermin.
Geometri yang direfleksikan berhadapan dengan petanya.

Sebagai contoh:

refleksi

Bentuk refleksi terhadap berbagai garis sebagai berikut:

Titik		Garis/Kurva		Gambar Refleksi
Awal	Bayangan	Awal	Bayangan	Gambar Refleksi
Refleksi sumbu y
A(x, y)	AI (-x, y)	y = f(x)	yI = f(-x)
Refleksi sumbu y = h
A(x, y)	AI (x, 2h – y)	y = f(x)	yI = 2h – f(x)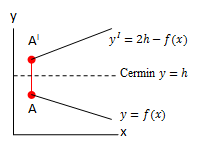
Refleksi sumbu x = h
A(x, y)	AI (2h – x, y)	y = f(x)	yI = f(2h – x)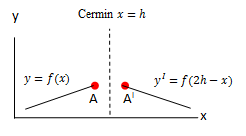
Refleksi sumbu y = x
A(x, y)	AI (y, x)	y = f(x)	x = f(y)
Refleksi sumbu y = -x
A(x, y)	AI (-y, -x)	y = f(x)	x = -f(-y)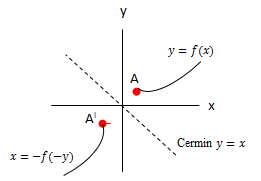
Refleksi terhadap titik O (0,0)
A(x, y)	AI (-x, -y)	y = f(x)	yI = -f(-x)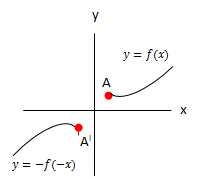

Selain refleksi terhadap garis diatas, titik dan kurva juga dapat direfleksikan terhadap suatu garis y=mx+k. Berikut refleksinya:

refleksi terhadap garis dan kurva

Dapat di gambarkan:

transformasi geometri pencerminan

Translasi

Translasi merupakan pergeseran atau pemindahan semua titik pada bidang geometri sejauh dan arah yang sama. Penulisan atau notasi translasi sama dengan notasi vektor. Jika titik B ditranslasi sampai titik $B^I$ maka dapat dinotasikan:

$\overrightarrow{BB^I}$

Sebagai contoh:

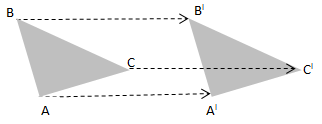
transformasi geometri bentuk translasi

Titik A, B, dan C, masing-masing ditranslasikan ke titik AI, BI, dan CI dengan jarak dan arah yang sama.

Suatu translasi dapat ditinjau terhadap sumbu x dan sumbu y. Pergeseran sejauh a sejajar sumbu x (bergeser ke kanan a>0, ke kiri a<0) dan pergeseran sejauh b sejajar sumbu y (bergeser ke atas b>0, ke bawah b<0) dinyatakan sebagai:

$T =\left(\begin{array}{r} a\\ b\end{array}\right)$

Dengan a dan b adalah komponen translasi. Bentuk-bentuk translasi sejauh $(\frac{a}{b})$ sebagai berikut:

Posisi Awal	Posisi Akhir	Pergeseran
Translasi Titik
A(x, y)	AI (x+a, y+b) Dengan x dan y adalah koordinat
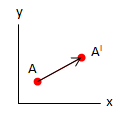Translasi Garis
mx+ny=c	m(x + a) + n(y + b) = c Dengan m dan n adalah koefisien dan c konstanta
Translasi Kurva
y = mx2+ kx + l	$(y+b) = m(x+a)^2 + k(x+a) + l$ Dengan m dan k adalah koefisien dan l konstanta
Translasi Lingkaran
x2 + y2 = c	$(x + a)^2 + (y + b)^2 = c$ Dengan c adalah konstanta

Evaluasi :
Agar kalian lebih memahami materi hari ini, Silahkan kalian kerjakan LKPD di bawah ini !

LKPD TRANSFORMASI GEOMETRI

Kesimpulan :

untuk kesimpulan materi hari ini, Refleksi atau pencerminan merupakan transformasi geometri berupa pergeseran atau pemindahan semua titik pada bidang geometri kearah sebuah garis atau cermin dengan jarak sama dengan dua kali jarak titik kecermin. Ada dua sifat penting dalam refleksi:

a. Jarak titik kecermin sama dengan jarak bayangan titik ke cermin.
b. Geometri yang direfleksikan berhadapan dengan petanya.

Sedangkan Translasi atau pergeseran merupakan pergeseran atau pemindahan semua titik pada bidang geometri sejauh dan arah yang sama.

Penulisan atau notasi translasi sama dengan notasi vektor. Jika titik B ditranslasi sampai titik $B^I$ maka dapat dinotasikan:

$\overrightarrow{BB^I}$

Semoga dengan penjelasan dan contoh di atas , kalian akan bertambah ilmunya dan dapat memahami nya. Jika ada yang ingin ditanyakan silahkan isi kolom kometar di bawah ini..

Wassalamualaikum Warrohmatullahi Wabarrohkatuh..

Sumber :

https://www.ruangguru.com/blog/pengertian-dan-jenis-jenis-transformasi-geometri

https://www.bing.com/ck/a?!&&p=92ad2c75029c5336e01387437b5eb5bcc8658b8dace5e53560eac251f956b3c0JmltdHM9MTczNjIwODAwMA&ptn=3&ver=2&hsh=4&fclid=2db8745a-837b-6dd3-0482-67d782f56c57&u=a1aHR0cHM6Ly9pZC5zY3JpYmQuY29tL2RvY3VtZW50LzY4MTkwOTAxMC9Ma3BkLU1hdGVyaS1UcmFuc2Zvcm1hc2ktR2VvbWV0cmk&ntb=1

Faradibaarifin

Minggu, 12 Januari 2025

REFLEKSI DAN TRANSLASI

Refleksi

Translasi

Tidak ada komentar:

Posting Komentar

ROTASI DAN DILATASI

Laporkan Penyalahgunaan