IDENTITAS
Mata Pelajaran : Matematika
Kelas : IX C dan IX D
Pertemuan : Ke2
Materi : Kesebangunan
Guru Pengampu : Fara Dibah, S.Pd
Waktu Pembelajaran: Senin, 10 Februari 2025
Alat Peraga : Buku Berpetak, Pensil, Penggaris
Media Pembelajaran : LCD Proyektor dan Laptop
Kompetensi Dasar :
3.6 Menjelaskan Kesebangunan dan Kekongruenan4.6 Menyelesaikan masalah konstektual yang berkaitan dengan Kesebangunan dan Kekongruenan
Materi : Mengenal dan menyelesaikan masalah yang berkaitan dengan Kesebangunan
Tujuan :
1. Peserta didik dapat memahami tentang Kesebangunan dan penerapannya dalam kehidupan sehar-hari
2. Peserta didik dapat menyelesaikan masalah konstektual yang berkaitan dengan kesebangunan
Untuk pertemuan kali ini kita akan mempelajari tentang materi Kesebangunan dan lebih untuk jelas nya dalam memahami materi hari ini silahkan kalian baca dan pahami pembahasan materi berikut :
Pengertian Kesebangunan
Kesebangunan berasal dari kata sebangun yang artinya bangun yang sama. Kesebangunan dapat dilambangkan dengan tanda (~). Menurut para ahli, pengertian kesebangunan bangun datar ialah dua atau lebih bangun datar yang mempunyai perbandingan besar sudut dan panjang sisi sisinya. dua atua lebih bangun datar dapat dikatakan sebangun jika memiliki ciri ciri:
- Sudut sudut bangun datar sesuai dan sama besarnya.
- Setiap sisi baik panjang dan lebar memiliki perbandingan yang sama.
Berdasarkan syarat kesebangunan bangun datar diatas dapat disimpulkan bahwa meskipun dua buah bangun memiliki bentuk yang sama namun lebar dan panjang yang berbeda asalkan sesuai perbandinganya maka dua buah bangun tersebut dapat dikatakan sebangun atau memiliki sifat kesebangunan. Singkatnya rumus yang digunakan dalam kesebangunan tersebut hampir sama dengan rumus perbandingan senilai. Adapun rumus kesebangunan bangun datarnya yaitu:
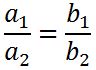
Agar kalian lebih memahami mengenai materi kesebangunan bangun datar tersebut. Perhatikan contoh kesebangunan bangun datar dalam bentuk soal yaitu sebagai berikut:
Contoh Soal Kesebangunan Bangun Datar
Perhatikan gambar di bawah ini!
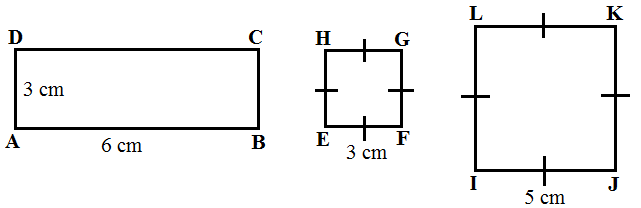
Berdasarkan gambar di atas, manakah bangun datar yang dapat dikatakan sebangun?
Jawab.
Kita dapat mengetahui jawaban materi kesebangunan bangun datar di atas dengan melakukan beberapa percobaan seperti di bawah ini:
Perhatikan Persegi Panjang ABCD dan Persegi EFGH
Panjang sisi pada bangun persegi panjang dan persegi di atas dapat dibentuk perbandingan seperti di bawah ini:
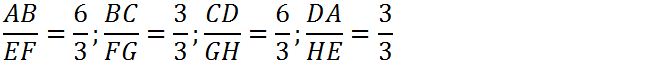
Dapat dilihat bahwa perbandingan panjang sisi pada bangun yang bersesuaian tidak sama. Dalam hal ini persegi panjang ABCD dan persegi EFGH tidak sebangun. Karena perbandingannya berbeda maka dengan kata lain persegi panjang ABCD dan persegi IJKL juga tidak sebangun. Meskipun besar sudut yang bersesuaian pada bangun persegi panjang ABCD dengan persegi EFGH dan persegi IJKL adalah sama.
Perhatikan Persegi EFGH dan Persegi IJKL
Panjang sisi pada bangun persegi EFGH dan persegi IJKL di atas dapat dibentuk perbandingan seperti di bawah ini:
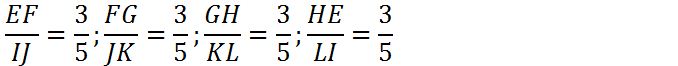
Dapat dilihat bahwa perbandingan panjang sisi pada bangun yang bersesuaian adalah sama. Dalam hal ini persegi EFGH persegi IJKL sebangun. Kemudian besar sudut yang bersesuaian pada bangun persegi EFGH dan persegi IJKL juga sama.
Jadi bangun datar yang dapat dikatakan sebangun ialah bangun datar persegi EFGH dan persegi IJKL.
Syarat-syarat Kesebangunan
Dalam konteks bangun datar, syarat kesebangunan bangun datar juga ada dua. Yaitu sudut-sudut yang bersesuaian harus sama besar dan sisi-sisi yang bersesuaian memiliki perbandingan yang sama.
Agar lebih jelas, perhatikan gambar berikut ini:
1. Sudut-sudut yang bersesuaian sama besar
Sama seperti syarat kongruen, dua objek yang sebangun harus memiliki sudut yang sama besar. Dalam gambar di atas, kamu bisa melihat kalau ∠A = ∠S, ∠B = ∠T, dan ∠C = ∠U.
2. Sisi-sisi yang bersesuaian memiliki perbandingan yang sama
Selain itu, sisi yang bersesuaian harus memiliki perbandingan yang sama. Untuk mengetahuinya, kamu bisa menghitung perbandingan setiap sisi yang bersesuaian. Sebagai contoh:
Sisi ST dan AB memiliki perbandingan yang sama atau dapat ditulis ST/AB = 3/6 = 1/2
Sisi TU dan BC memiliki perbandingan yang sama atau dapat ditulis TU/BC = 3/6 = 1/2
Sisi SU dan AC memiliki perbandingan yang sama atau dapat ditulis SU/AC = 3/6 = 1/2
Dari perhitungan tersebut diketahui kalau ST/AB = TU/BC = SU/AC . Ketiga pasang sisi-sisi yang bersesuaian pada gambar di atas memiliki perbandingan yang sama. Sehingga, segitiga ABC sebangun dengan segitiga STU. Namun, karena panjang sisinya berbeda, maka segitiga ABC tidak kongruen dengan segitiga STU.
Contoh Soal Kekongruenan Dan Kesebangunan
Agar lebih memahami materi kekongruenan dan kesebangunan, kamu bisa mencoba dan memperhatikan contoh soal kekongruenan dan contoh soal kesebangunan berikut ini:
1. Ganta memiliki tinggi badan 150 cm. Kemudian, Ganta berdiri dengan jarak sekitar 10 m dari suatu gedung. Ujung bayangan Ganta berimpit dengan ujung bayangan gedung. Jika panjang bayangan Ganta adalah 4 m, hitunglah tinggi gedung tersebut menggunakan rumus kekongruenan dan kesebangunan.
Pembahasan:
Agar lebih sederhana, buat gambar seperti ini terlebih dahulu:
Dari gambar tersebut, terlihat kalau segitiga ABE dan segitiga ACD telah memenuhi syarat segitiga sebangun. Sehingga, EB/DC = AB/AC. Kemudian, kamu tinggal memasukkan angka yang ada ke dalam rumus. Sebelum itu kamu dapat menuliskan informasi pada soal terlebih dahulu agar memudahkan kamu dalam pengerjaannya.
Diketahui
AB = 4 m; AC = 4 + 10 = 14 m; EB = 150 cm = 1,5 m;
Untuk mencari tinggi gedung kamu harus mencari nilai DC = …?
Selanjutnya masukkan nilai di atas ke dalam rumus berikut.
EB/DC = AB/AC
1,5 / DC = 4 / 14
DC = (1,5 x 14) / 4
DC = 21 / 4
DC = 5,25 m
Jadi, tinggi gedung adalah 5,25 meter.
2. Perhatikan gambar berikut ini!
Jika P dan Q merupakan titik tengah diagonal BD dan AC, berapa panjang PQ?
A. 2 cm
B. 3 cm
C. 4 cm
D. 5 cm
Pembahasan:
Ingat, setiap mengerjakan soal, tuliskan informasi pada soal terlebih dahulu agar kamu mudah mengerjakannya. Nah, Untuk menjawab soal ini, kamu bisa menggunakan rumus cepat dari kekongruenan dan kesebangunan, yaitu PQ = 1/2 (DC – AB). Sehingga,
PQ = 1/2 (12 – 6)
PQ = 1/2 x 6
PQ = 3 cm
Sehingga, jawabannya adalah B. 3 cm.
Untuk kesimpulan pada pembelajaran hari ini, bahwa
Kesebangunan dapat dilambangkan dengan tanda (~). Menurut para ahli, pengertian kesebangunan bangun datar ialah dua atau lebih bangun datar yang mempunyai perbandingan besar sudut dan panjang sisi sisinya. dua atua lebih bangun datar dapat dikatakan sebangun jika memiliki ciri ciri:
- Sudut sudut bangun datar sesuai dan sama besarnya.
- Setiap sisi baik panjang dan lebar memiliki perbandingan yang sama.
Berdasarkan syarat kesebangunan bangun datar diatas dapat disimpulkan bahwa meskipun dua buah bangun memiliki bentuk yang sama namun lebar dan panjang yang berbeda asalkan sesuai perbandinganya maka dua buah bangun tersebut dapat dikatakan sebangun atau memiliki sifat kesebangunan. Singkatnya rumus yang digunakan dalam kesebangunan tersebut hampir sama dengan rumus perbandingan senilai
https://www.antotunggal.com/2021/11/materi-kesebangunan-bangun-datar.htmlhttps://www.pijarbelajar.id/blog/kekongruenan-dan-kesebangunan

Tidak ada komentar:
Posting Komentar