KONSEP KEKONGRUENAN

MATA PELAJARAN : MATEMATIKA

KELAS : IX D,E, F

WAKTU PEMBELAJARAN : 

KELAS IX F : 30 JANUARI 2023

KELAS IX D, E : 01 FEBRUARI 2023


KOMPETENSI DASAR :

3.6       Menjelaskan dan menentukan kesebangunan dan kekongruenan antar bangun datar

4.6       Menyelesaikan masalah yang berkaitan dengan kesebangunan dan kekongruenan antar bangun datar


TUJUAN PEMBELAJARAN :

Setelah mengikuti pembelajaran, Peserta didik diharapkan dapat :

1. Memahami konsep kekongruenan pada bangun datar

2. Menyelesaikan masalah yang berkaitan dengan kekongruenan antar bangun datar


MATERI PEMBELAJARAN :

 Kekongruenan

Dua bangun yang mempunyai bentuk dan ukuran yang sama dinamakan kongruen. Jika kita hubungkan dengan materi sebelumnya yaitu transformasi, maka kita bisa katakan bahwa semua bangun datar yang  ditransformasi dengan cara refleksi, translasi dan rotasi memiliki sifat kekongruenan. 

Syarat Dua Bangun Datar Kongruen :

Dua bangun segi banyak (poligon) dikatakan kongruen jika memenuhi dua syarat, yaitu:

(i) sisi-sisi yang bersesuaian sama panjang, dan

(ii) sudut-sudut yang bersesuaian sama besar

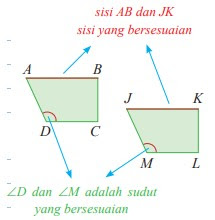
Sudut-sudut yang bersesuaian:

 ∠A dan ∠J → m∠A = m∠J

 ∠B dan ∠K → m∠B = m∠K

 ∠C dan ∠L → m∠C = m∠L

 ∠D dan ∠M → m∠D = m∠M

Sisi-sisi yang bersesuaian:

 AB dan JK → AB = JK

 BC dan KL → BC = KL

 CD dan LM → CD = LM

 DA dan MJ → DA = MJ

 

Jika bangun ABCD dan JKLM memenuhi kedua syarat tersebut, maka bangun ABCD dan JKLM kongruen, dinotasikan dengan ABCD ≅ JKLM. Jika bangun ABCD dan JKLM tidak memenuhi kedua syarat tersebut maka bangun ABCD dan JKLM tidak kongruen, dinotasikan dengan ABCD ≅ JKLM.
 

Contoh Soal :

1. Segi empat ABCD dan WXYZ pada gambar di bawah kongruen. Manakah sisi-sisi dan sudut-sudut yang bersesuaian?
Segi empat ABCD dan WXYZ

 

Alternatif Penyelesaian:


 

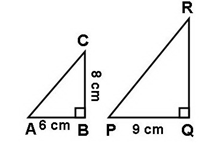
2. Manakah persegi di bawah yang kongruen? Jelaskan!


  

Alternatif Penyelesaian:

Dua bangun dikatakan kongruen jika memenuhi dua syarat, yaitu:

(i) sudut-sudut yang bersesuaian sama besar Setiap persegi mempunyai empat sudut siku-siku, sehingga sudut-sudut yang bersesuaian pada persegi (a), (b) dan (c) besarnya pasti sama.

(ii) sisi-sisi yang bersesuaian sama panjang

Persegi (a) dan persegi (b)

Panjang setiap sisi persegi (a) adalah 8 cm. Panjang setiap sisi persegi (b) adalah 9 cm. Jadi, sisi-sisi yang bersesuaian persegi (a) dan (b) tidak sama panjang.

Persegi (b) dan persegi (c)

Panjang setiap sisi persegi (b) adalah 9 cm. Panjang setiap sisi persegi (c) adalah 8 cm. Jadi, sisi-sisi yang bersesuaian persegi (b) dan (c) tidak sama panjang.

Persegi (a) dan persegi (c)

Panjang setiap sisi persegi (a) adalah 8 cm. Panjang setiap sisi persegi (c) adalah 8 cm.

Jadi, sisi-sisi yang bersesuaian persegi (a) dan (c) sama panjang. Berdasarkan (i) dan (ii) di atas, maka persegi yang kongruen adalah persegi (a) dan (c).

 

3. Perhatikan gambar trapesium ABCD dan PQRS yang kongruen di bawah ini.

 

a. Jika panjang sisi AB = 40 cm, BC = 21 cm, RS = 16 cm, dan PS = 15 cm, tentukan panjang sisi AD, DC, PQ, dan QR.

b. Jika besar ∠A = 60o , ∠B = 40o . Berapakah besar ∠R dan ∠S? (selanjutnya, besar ∠A ditulis dengan m∠A, seperti yang sudah kamu kenal di kelas 7 dan 8)

Alternatif Penyelesaian:

Diketahui: bangun ABCD ≅ PQRS, berarti

    sisi-sisi yang bersesuaian sama panjang
    sudut-sudut yang bersesuaian sama besar

a. Untuk menentukan panjang sisi AD, DC, PQ, dan QR, tentukan terlebih dulu sisisisi yang bersesuaian yaitu:

(mengapa bukan AB = SR? Jelaskan)

Dengan demikian, jika AB = 40 cm, BC = 21 cm, RS = 16 cm, dan PS = 15 cm maka:

AD = PS = 15 cm

DC = SR = 16 cm

QR = BC = 21 cm

PQ = AB = 40 cm

b. Untuk menentukan m∠R dan m∠S, tentukan terlebih dulu sudut-sudut yang bersesuaian yaitu:

Dengan demikian, jika m∠A = 60o , m∠B = 40o maka:

m∠P = m∠A = 60o dan

m∠Q = m∠B = 40o

m∠R + m∠Q = 180o

m∠R = 180o – m∠Q

m∠R = 180o – 40o

m∠R = 140o

m∠S = 180o – m∠P

m∠S = 180o – 60o

m∠S = 120o Jadi

m∠R = 140o dan m∠S = 120o .

MENENTUKAN PANJANG SISI & SUDUT KESEBANGUNAN

MATA PELAJARAN : MATEMATIKA

KELAS : IX D, E, F

WAKTU PEMBELAJARAN : 16 - 18 JANUARI 2023

KOMPETENSI DASAR :

3.6       Menjelaskan dan menentukan kesebangunan dan kekongruenan antar bangun datar

4.6       Menyelesaikan masalah yang berkaitan dengan kesebangunan dan kekongruenan antar bangun datar

TUJUAN PEMBELAJARAN :

Setelah mengikuti pembelajaran, Peserta didik diharapkan dapat :

1. Menentukan panjang sisi dan besar sudut yang belum diketahui

2. Menyelesaikan masalah yang berkaitan dengan kesebangunan antar bangun datar 

MATERI PEMBELAJARAN :

Syarat Kesebangunan Bangun Datar

Dua bangun datar yang mempunyai bentuk yang sama disebut sebangun. Tidak perlu ukurannya sama, tetapi sisi-sisi yang bersesuaian sebanding (proportional) dan sudut-sudut yang bersesuaian sama besar. Perubahan bangun satu menjadi bangun lain yang sebangun melibatkan perbesaran atau pengecilan. 

Dengan kata lain dua bangun dikatakan sebangun jika memenuhi syarat:

(i) perbandingan panjang sisi yang bersesuaian senilai

(ii) sudut yang bersesuaian besarnya sama

m∠A = m∠E

m∠B = m∠F

m∠C = m∠G

m∠D = m∠H

Jika bangun ABCD dan EFGH memenuhi kedua syarat tersebut, maka bangun ABCD dan EFGH sebangun, dinotasikan dengan ABCD ∼ EFGH. 

Jika bangun ABCD dan EFGH tidak memenuhi kedua syarat tersebut maka bangun ABCD dan EFGH tidak sebangun, dinotasikan dengan ABCD ≁ EFGH. 

Contoh Soal

Perhatikan gambar di bawah ini. 

Bangun ABCD dan EFGH

Bangun ABCD dan EFGH sebangun. 

Tentukan nilai x, y dan z!

Alternatif Penyelesaian: 

Bangun ABCD dan EFGH sebangun berarti sudut-sudut yang bersesuaian sama besar dan perbandingan sisi-sisi yang bersesuaian senilai, yaitu: 

m∠E = m∠A, m∠F = m∠B, m∠G = m∠C, m∠H = m∠D, 

Perbandingan sisi bangun datar

Bangun ABCD dan EFGH sebangun dengan sudut-sudut yang bersesuaian m∠E = m∠A, m∠F = m∠B, m∠G = m∠C, dan m∠H = m∠D, 

Sehingga,

m∠G = m∠C ⇔ xo = 22,6o 

m∠D = 180o – m∠C ⇔ yo = 180o – xo = 180o – 22,6o = 157,4o (Mengapa?) 

m∠H = m∠D ⇔ zo = yo = 157,4o 

Jadi, nilai adalah xo = 22,6o , yo = 157,4o , dan zo = 157,4o

Penugasan materi :

Latihan Soal 4.3 hal 108 no. 2

SIFAT DAN LUAS KESEBANGUNAN DUA SEGITIGA

 Nama Guru : Fara Dibah, S.Pd

Mapel         : Matematika

Kelas         : IX D, E, F

Rabu - Kamis, 11 - 12 Januari 2023

Kompetensi Dasar :

3.6       Menjelaskan dan menentukan kesebangunan dan kekongruenan antar bangun datar

4.6       Menyelesaikan masalah yang berkaitan dengan kesebangunan dan kekongruenan antar bangun datar

 

Materi : Sifat-Sifat dan Luas Kesebangunan Dua Segitiga

 

Tujuan Pembelajaran :

 Setelah mengikuti pembelajaran, Siswa diharapkan dapat :

1. Mencermati ukuran sisi dan sudut (sifat-sifat) pada segitiga yang sebangun.

2. Mengidentifikasi perbandingan sisi dan sudut antar segitiga yang sebangun.

3. menghitung panjang sisi dan luas pada segitiga yang sebangun  

 

Assalamualaikum Warrohmatullahi  Wabbarokatuh..

Selamat pagi Semua !
Bagaimana Kabar Soleh/Soleha hari ini ?…
Semoga kita semua dalam lindungan Allah SWT. Aamiin ..

Soleh/soleha apakah tadi subuh kalian sudah melaksanakan solat subuh tepat waktu ? untuk yang laki-laki solat subuh nya di masjid atau di musholla ya nak, agar kita mendapat keberkahan dari Allah SWT ..
Dan untuk yang perempuan silahkan solat subuh nya secara munfarid dirumah masing-masing..

 

Baiklah soleh/soleha, hari ini kita memasuki materi selanjutnya yaitu Sifat-Sifat dan Luas Kesebangunan Dua Segitiga..
Untuk lebih jelasnya silahkan kalian simak materi berikut ini ..

Perhatikan gambar berikut.

       

Diketahui ΔABC sebangun dengan ΔKLM. Untuk membuktikan kesebangunan kedua segitiga tersebut, bandingkan sisi-sisi dan sudut-sudut yang bersesuaian. Untuk membandingkan sisi–sisi yang bersesuaian (seletak), perhatikan sisi di depan sudut yang berukuran sama. Dari gambar di atas, perbandingan sisi yang bersesuaian pada segitiga ABC dan KLM yaitu:
BCLM=CAMK=ABKL
⇔a2a=b2b=c2c=12
Selain itu, dari sudut-sudut yang bersesuaian diperoleh:
∠ACB = ∠ KML
∠CAB = ∠MKL
Ini berarti, ∠ABC = ∠KLM
Berdasarkan uraian di atas, diperoleh kesimpulan sebagai berikut.

Sifat–Sifat Segitiga yang Sebangun :

    1. Sisi-sisi yang bersesuaian mempunyai perbandingan yang senilai.
    2. Sudut–sudut yang bersesuaian sama besar.

Untuk memeriksa kesebangunan pada segitiga, lakukan pengujian terhadap unsur-unsur yang diketahui berdasarkan syarat-syarat kesebangunan segitiga pada tabel di bawah ini.

 

Contoh 1
Perhatikan gambar berikut.

Jika segitiga ABC sebangun dengan DEF, maka tentukan panjang sisi EF.
 

Penyelesaian:

 
Diketahui:
panjang sisi AB = 5 cm
panjang sisi BC = 4 cm
panjang sisi DE = 30 cm
ABDE=BCEF
⇔530=4EF
⇔16=4EF
⇔EF=24
Jadi, panjang sisi EF adalah 24 cm.

Contoh 2
Perhatikan gambar berikut.

Tentukan syarat-syarat yang dipenuhi agar ΔABC sebangun dengan ΔADE.
 

Penyelesaian:

 
ΔABC sebangun dengan ΔADE karena:

    ∠BAC berimpit dengan ∠DAE sehingga besarnya sama.
    besar ∠ABC = ∠ADE karena keduanya adalah sudut-sudut sehadap.
    besar ∠ACB = ∠AED karena keduanya adalah sudut-sudut sehadap.

Jadi, ΔABC sebangun dengan ΔADE karena memenuhi syarat sudut, sudut, sudut (sd, sd, sd).
 

Contoh 3
Perhatikan gambar berikut.

Jika ΔABC sebangun dengan ΔPQR, maka tentukan:

    syarat yang dipenuhi agar segitiga tersebut sebangun.
    panjang sisi QR.
    panjang sisi PR

Penyelesaian:
Diketahui:
ΔABC sebangun dengan ΔPQR
panjang sisi AB = 6 cm
panjang sisi BC = 8 cm
∠ABC = 90⁰ (sudut siku-siku)
panjang sisi PQ = 9 cm
∠PQR = 90⁰ (sudut siku-siku)

    Syarat yang dipenuhi agar ΔABC sebangun dengan ΔPQR

Ini berarti:
sisi AB bersesuaian dengan PQ
sisi BC bersesuaian dengan QR
∠ABC bersesuaian dengan ∠PQR
 

Jadi, syarat yang memenuhi segitiga tersebut sebangun adalah sisi, sudut, sisi (s, sd, s).

    Panjang sisi QR

Tentukan perbandingan sisi-sisi yang bersesuaian pada ΔABC dan ΔPQR.
ABPQ=BCQR=ACPR
Panjang sisi QR adalah:
ABPQ=BCQR
⇔69=8QR
⇔23=8QR
⇔2QR=24
⇔QR=12
Jadi, panjang QR = 12 cm.

    Panjang sisi PR

Panjang sisi PR dapat ditentukan dengan menggunakan teorema Pythagoras.
PR2 = PQ2 + QR2
⇔ PR2 = 92 + 122
⇔ PR2 = 81 + 144
⇔ PR2 = 225
⇔ PR = 15
Jadi, panjang sisi PR adalah 15 cm.

 

Alhamdulillah kalian sudah mengikuti pembelajaran dan menyimak materi hari ini.
Coba agar lebih memahami lagi, silahkan kalian lakukan Latihan 4.3 Halaman 113 pada buku Besar dan silahkan kalian diskusikan dengan teman-temanmu..

Thank you for today..
Semangat selalu para pejuang pencari Ilmu dan Ridho nya Allah untuk anak-anak Soleh/Soleha ibu ..
See you next time, and bye bye ...............

 
Wassalamualaikum Warromatullahi Wabarrohkatuh..

SEGITIGA-SEGITIGA SEBANGUN

Guru            : Fara Dibah, S.Pd

Mapel          : Matematika

Kelas           : IX D, E, F

Senin - Rabu, 09 - 11 Januari 2023

Kode KD     :

3.6       Menjelaskan dan menentukan kesebangunan dan kekongruenan antar bangun datar

4.6       Menyelesaikan masalah yang berkaitan dengan kesebangunan dan kekongruenan antar bangun datar

 

Materi          : Segitiga-segitiga Sebangun

Tujuan          : 

Setelah mengikuti pembelajaran, siswa diharapkan dapat :

1. Menjelaskan Kesebangunan dua bangun datar

2. Mengidentifikasi benda di sekitar yang berkaitan dengan kesebangunan bangun datar 

3. Mencermati ukuran sisi dan sudut pada bangun datar yang sebangun 

4. Mengidentifikasi perbandingan sisi dan sudut antara bangun datar sebangun

5. Menganalisis hubungan antara luas bangun dengan panjang sisi antara bangun yang sebangun

 

Assalamualaikum Warromatullahi Wabarrohkatuh..

Selamat pagi Semua !

Bagaimana Kabar Soleh/Soleha hari ini ?…

Semoga kita semua dalam lindungan Allah SWT. Aamiin ..

Soleh/soleha apakah tadi subuh kalian sudah melaksanakan solat subuh tepat waktu ? untuk yang laki-laki solat subuh nya di masjid atau di musholla ya nak, agar kita mendapat keberkahan dari Allah SWT ..

Dan untuk yang perempuan silahkan solat subuh nya secara munfarid dirumah masing-masing..

Baiklah soleh/soleha, hari ini kita memasuki materi selanjutnya yaitu SEGITIGA-SEGITIGA YANG SEBANGUN..

Untuk lebih jelasnya silahkan kalian simak materi berikut ini ..

 

 

 Dua segitiga dikatakan sebangun jika hanya jika memenuhi syarat berikut ini.
(i) Perbandingan sisi-sisi yang bersesuaian senilai.
(ii) Besar sudut-sudut yang bersesuaian sama

  

 

 

 

Jika ∆ABC dan ∆A'B'C' memenuhi syarat tersebut, maka ∆ABC dan ∆A'B'C' sebangun, dinotasikan dengan ∆ABC ∼ ∆A'B'C'.
Jika ∆ABC dan ∆A'B'C' tidak memenuhi syarat, tersebut maka ∆ABC dan ∆A'B'C' tidak sebangun, dinotasikan dengan ∆ABC ≁ ∆A'B'C'.

Syarat Dua Segitiga Sebangun 

Untuk lebih sederhana, berdasarkan Kegiatan 2, dua segitiga dikatakan sebangun (misal: ∆ABC ∼ ∆A'B'C'), jika memenuhi salah satu kondisi berikut ini. 

1. Perbandingannya ketiga pasangan sisi yang bersesuaian sama, yaitu:

 

 

 

 2. Dua pasang sudut yang bersesuaian sama besar.
Contoh: m∠A = m∠A' dan m∠B = m∠B'

 

 3. Perbandingan dua pasang sisi yang bersesuaian sama dan sudut yang diapitnya sama besar.

 

 

 

agar dapat lebih kalian pahami, maka silahkan tonton dan simak video berikut :

                        Sumber : https://www.youtube.com/watch?v=5fgfvlxQ01k

 

 
 

 Alhamdulillah kalian sudah mengikuti pembelajaran dan menyimak materi hari ini.
Coba agar lebih memahami lagi, silahkan kalian lakukan Latihan 4.2 Halaman 108 pada buku Besar dan silahkan kalian diskusikan dengan teman-temanmu..

Thank you for today..
Semangat selalu para pejuang pencari Ilmu dan Ridho nya Allah untuk anak-anak Soleh/Soleha ibu ..
See you next time, and bye bye ...............

 
Wassalamualaikum Warromatullahi Wabarrohkatuh..